möchte­gern­geek

Die Frage wie groß das Revier eines Tieres ist, ist in konkreten Fällen für Biologen interessant und dank GPS-Sendern kann man es heutzutage sogar empirisch untersuchen. Aus der Punktwolke der besuchten Orte kann man eine Fläche abschätzen — im einfachsten Fall indem man die konvexe Hülle um alle besuchten Orte zeichnet.

Als Physiker sind mir echte Tiere zu kompliziert, sodass ich stattdessen annehme, dass sie punktförmig sind und ihre Bewegung ein Random Walk in einer isotropen Umgebung ist. Also springen meine idealisierten Tiere unabhängig von ihren bisherigen Handlungen zu ihrem nächsten Aufenthaltsort — der Abstand vom aktuellen Punkt ist dabei in jeder Dimension unabhängig und normalverteilt.

In jeder Dimension? Ja, genau! Wir wollen schließlich auch das Revierverhalten von vierdimensionalen Space Whales untersuchen.

Spaß beiseite, in dieser Veröffentlichung geht es natürlich eher um fundamentale Eigenschaften von Random Walks — einer der einfachsten und deshalb am besten untersuchten Markow-Prozesse. Und zwar im Hinblick auf Large Deviations, die extrem unwahrscheinlichen Ereignisse, die weit jenseits der Möglichkeiten von konventionellen Sampling-Methoden liegen. Details hierzu sind am besten direkt im Artikel oder mit einer Menge Hintergrundinformationen und ausführlicher als für ein Blog angemessen in dem entsprechenden Kapitel und Anhang meiner Dissertation nachzulesen. Insbesondere ist dort auch beschrieben wie die geometrischen Unterprobleme effizient gelöst werden können, auf die wir im Verlauf dieses Blogposts stoßen werden.

Das Problem eine konvexe Hülle zu finden ist einerseits einfach zu begreifen, schön geometrisch und sehr gut untersucht. Dadurch sind überraschend viele Algorithmen bekannt, die unterschiedliche Vor- und Nachteile haben.

Im Folgenden möchte ich deshalb ein paar Methoden vorstellen, wie man effizient die konvexe Hülle einer Punktmenge bestimmen kann, und dies mit animierten gifs von Punkten und Strichen visualisieren. Der Code zur Erstellung der Visualisierungen ist übrigens in Rust geschrieben und auf GitHub zu finden.

Andrew’s Monotone Chain

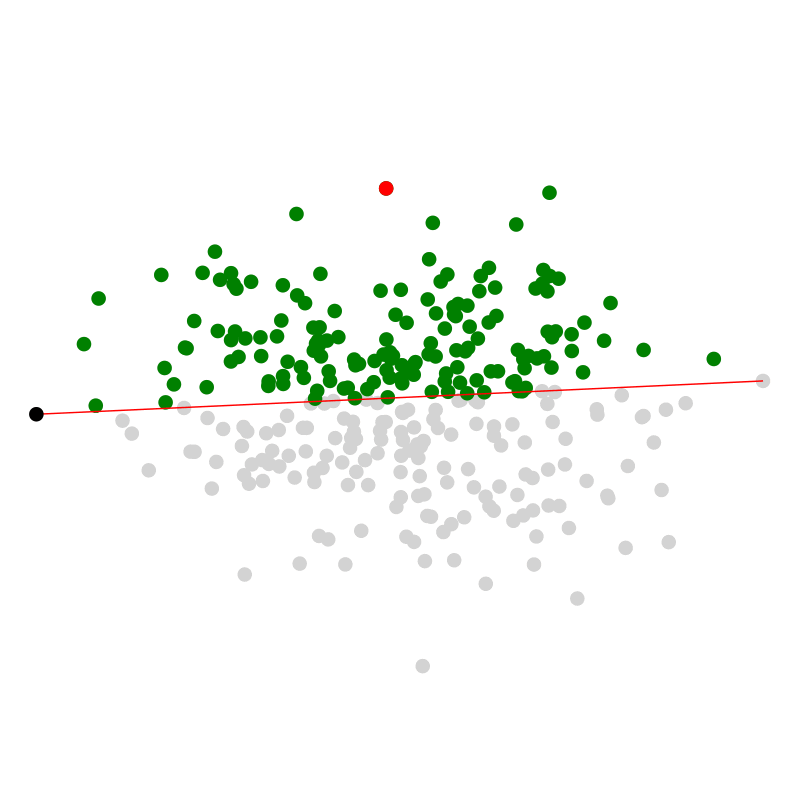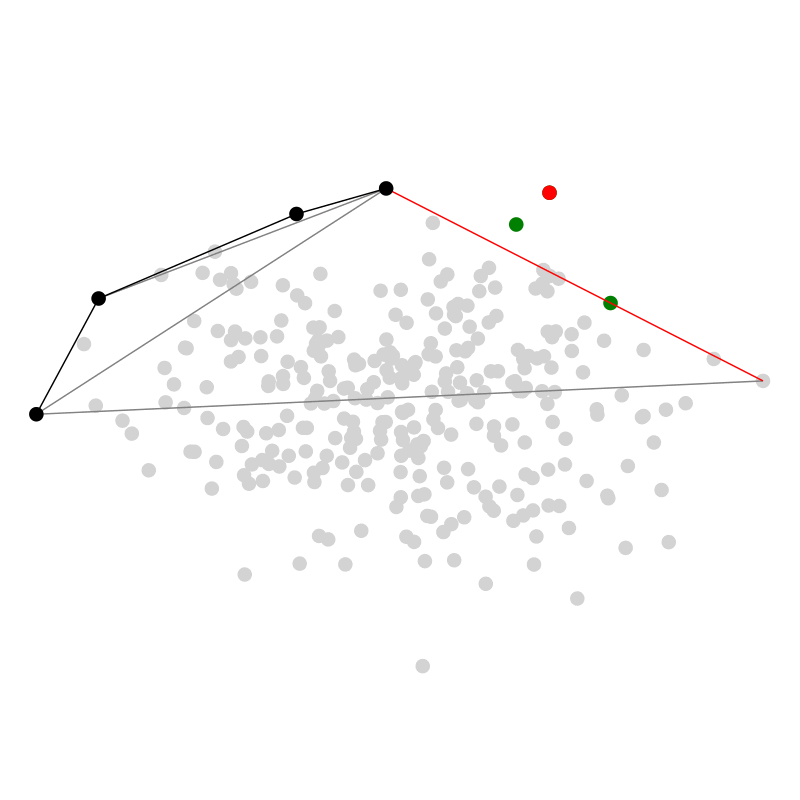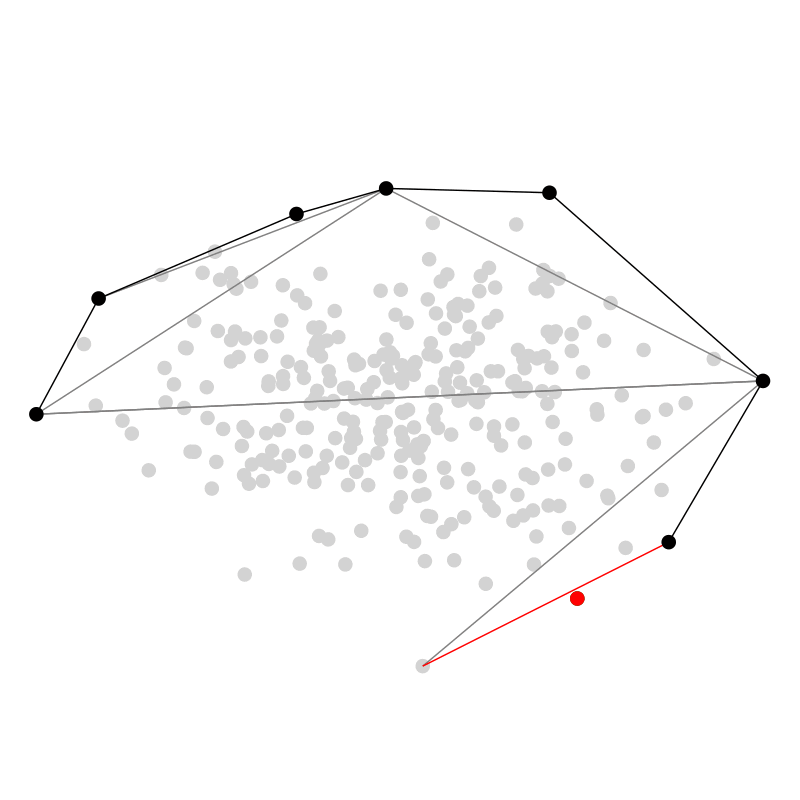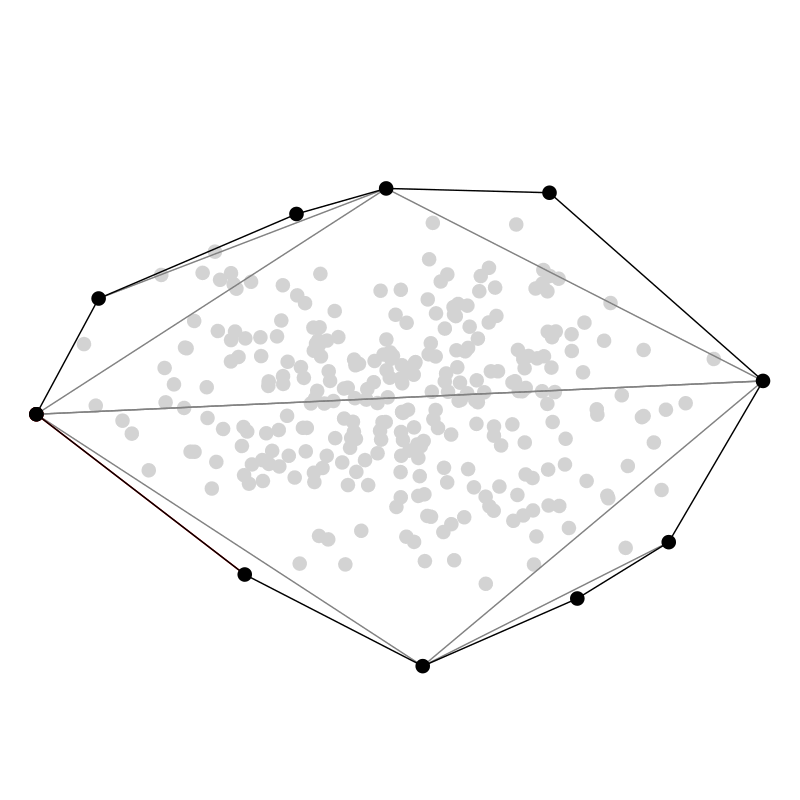
In zwei Dimensionen kann man ausnutzen, dass die konvexe Hülle ein Polygon ist, das man durch die Reihenfolge der Eckpunkte definieren kann. Die grundlegende Idee ist also die Punkte im Uhrzeigersinn zu sortieren, in dieser Reihenfolge, mit dem Punkt ganz links startend, alle zu einem Polygon hinzuzufügen und dabei darauf zu achten, dass die drei neusten Punkte des Polygons ein negativ orientiertes Dreieck bilden, also dass sie im „Uhrzeigersinn drehen“. Wenn das nicht der Fall ist, wird der mittlere Punkt entfernt.

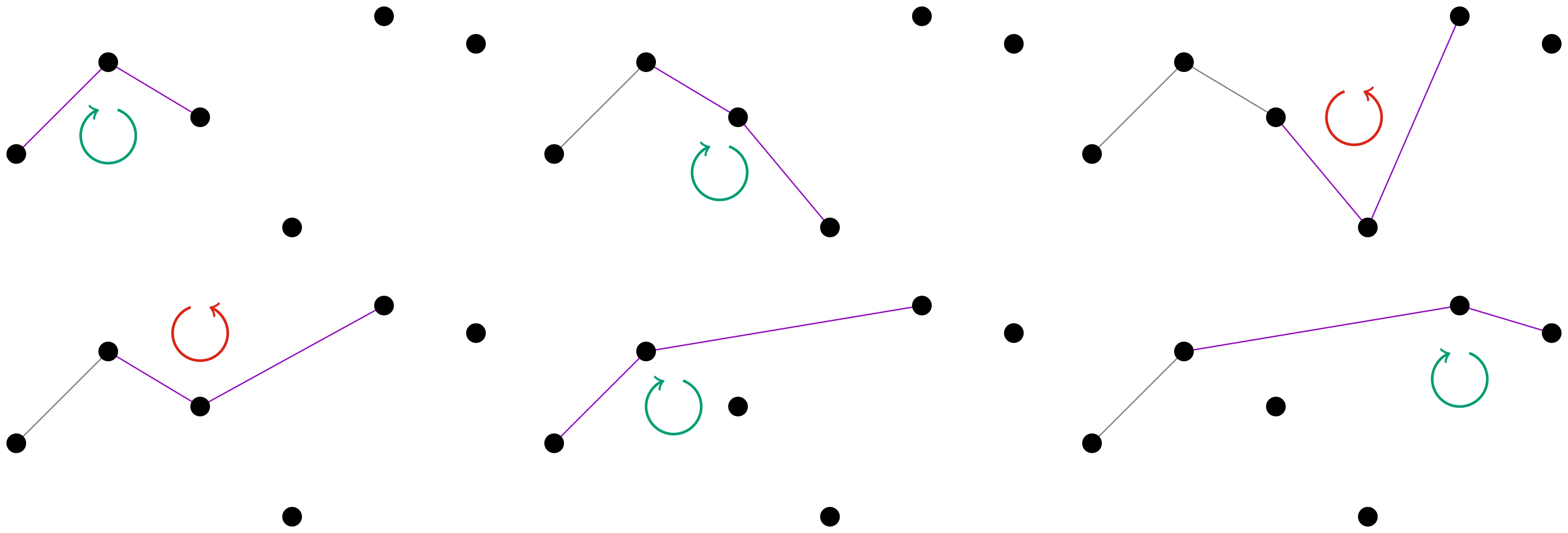
Dies ist übrigens die ursprüngliche Variante, der Graham Scan. Andrew verbesserte diesen Algorithmus dadurch, dass nicht im Uhrzeigersinn sortiert werden muss, sondern man lexikographisch nach horizontaler Koordinate (bei Gleichstand entscheidet die vertikale Koordinate) sortiert. Dann bildet dieser Algorithmus die obere Hälfte der Hülle und wenn man ihn rückwärts auf die sortierten Punkte anwendet, die untere Hälfte.

Die Komplexität für \(n\) Punkte ist somit \(\mathcal{O}(n \ln n)\) limitiert durch das Sortieren.

Jarvis March: Gift Wrapping

Ein Geschenk einzupacken ist ein relativ intuitiver Prozess: Wir bewegen das Papier so lange herunter, bis wir auf einen Punkt des Geschenkes treffen, wo es hängen bleibt Dann wickeln wir weiter, bis wir auf den nächsten Punkt stoßen. Dabei streben wir an die konvexe Hülle zu finden, denn sie ist das Optimum möglichst wenig Papier zu verbrauchen während wir die Punktwolke einhüllen, die wir verschenken wollen. Und offenbar klappt das auch in drei Dimensionen!

In einem Computer ist es allerdings einfacher das Geschenkpapier von innen aus der Punktwolke heraus nach außen zu falten. Für jede Facette testen wir also jeden der \(n\) Punkte in der Punktwolke darauf, ob er links von unserem Stück Geschenkpapier liegt. Wenn ja, falten wir das Papier weiter. Sobald wir alle \(n\) Punkte ausprobiert haben, wissen wir, dass das Geschenkpapier an der richtigen Stelle liegt, sodass anfangen können die nächste Facette mit dem Geschenkpapier zu bilden indem wir von innen alle Punkte durchtesten.

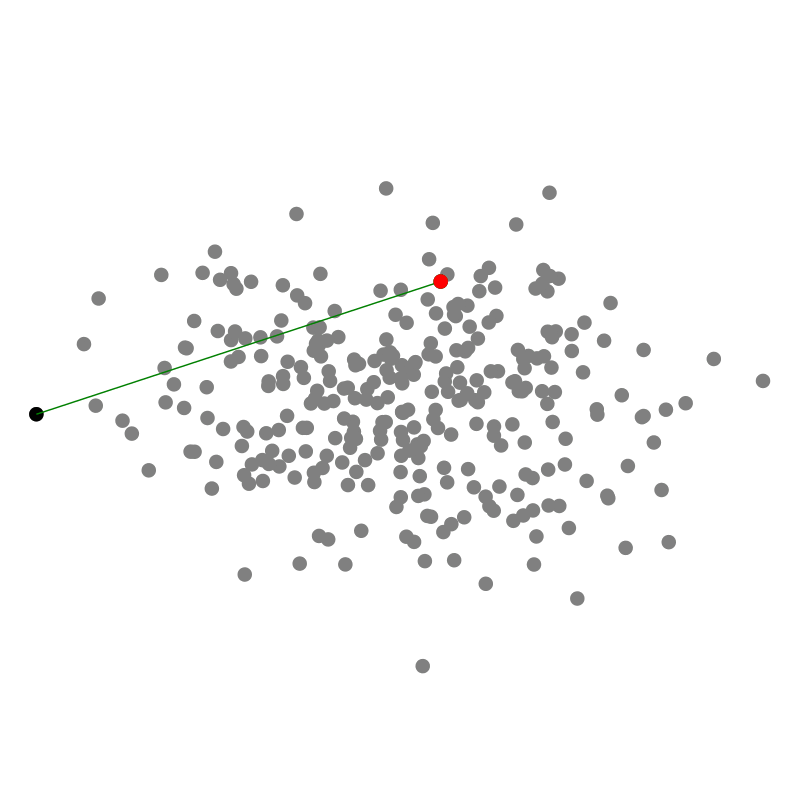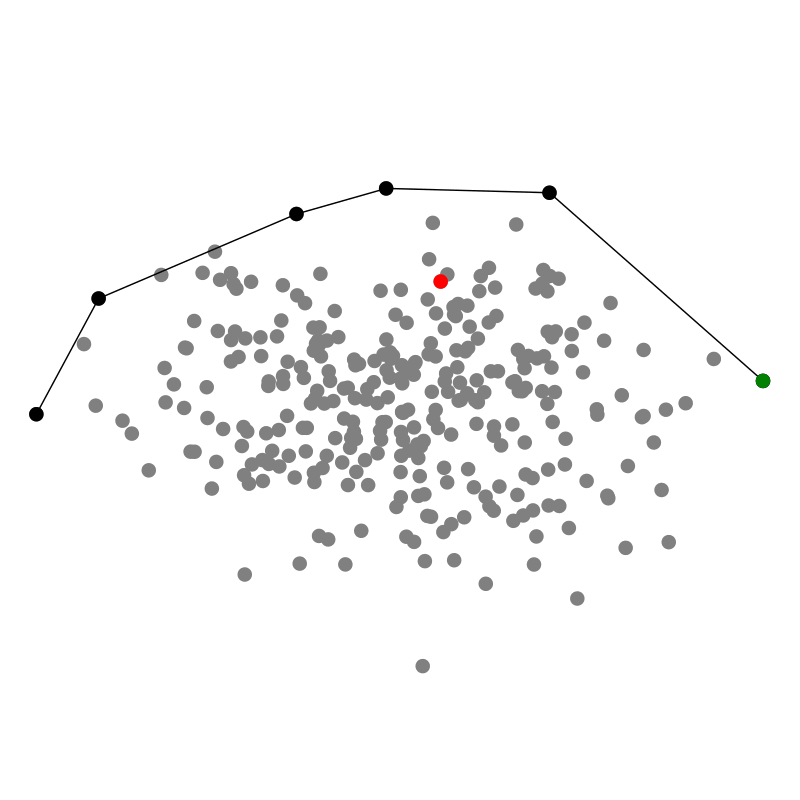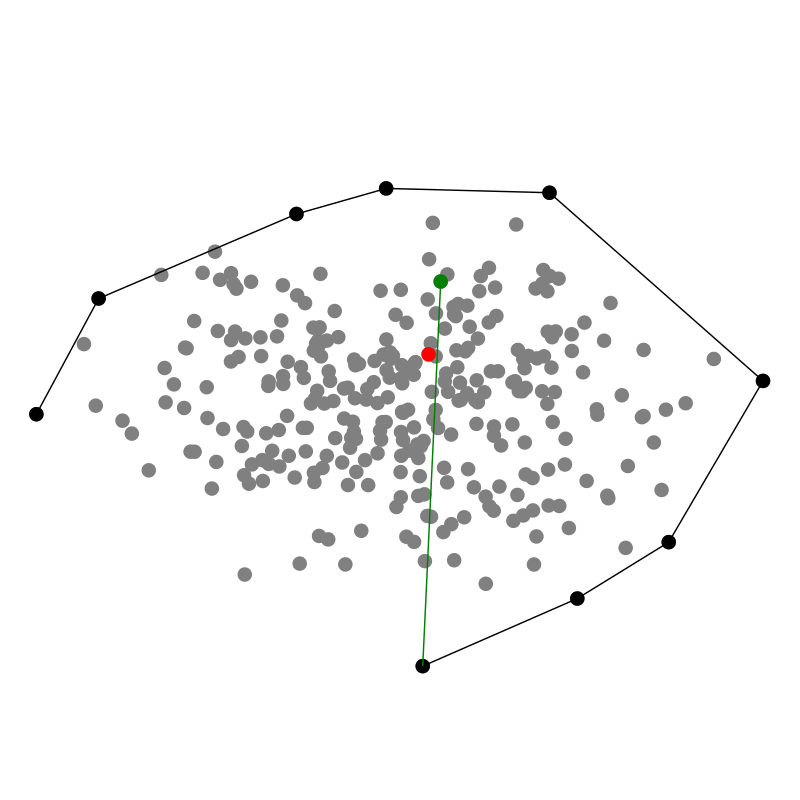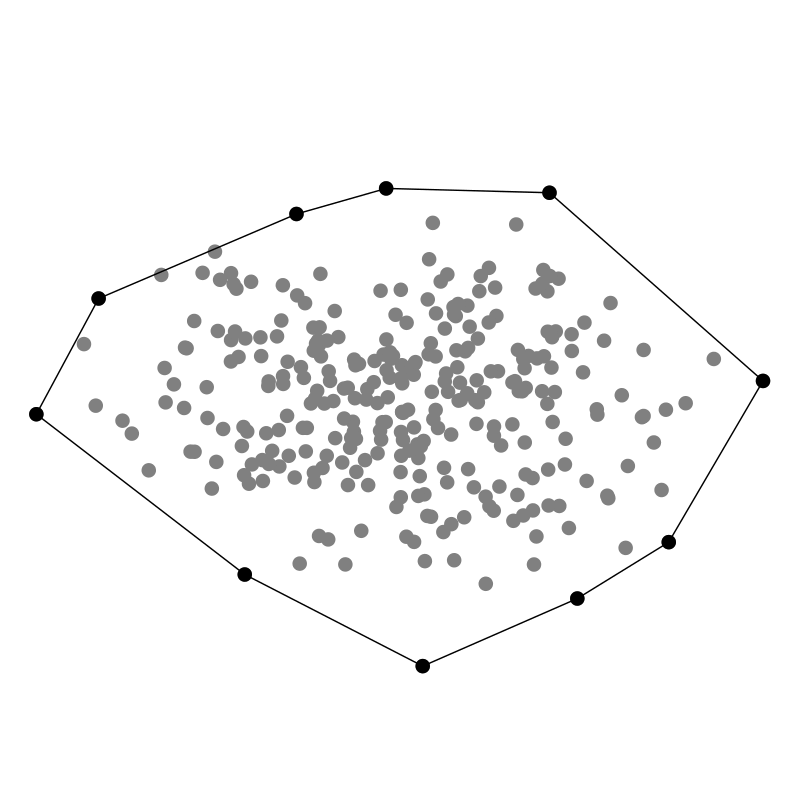
Interessanterweise müssen wir also für jeden der \(h\) Punkte, die zur Hülle gehören \(\mathcal{O}(n)\) Punkte prüfen, sodass die Komplexität abhängig ist vom Ergebnis: \(\mathcal{O}(n h)\)

Chan’s Algorithm

Wir haben also einen \(\mathcal{O}(n \ln n)\) und einen \(\mathcal{O}(n h)\) Algorithmus kennen gelernt, aber können wir noch besser werden? Ja! \(\mathcal{O}(n \ln h)\) ist die theoretische untere Komplexitätsgrenze für 2D konvexe Hüllen. Beispielsweise Chans Algorithmus erreicht diese Komplexität mit einem trickreichen zweistufigen Prozess.

Zuerst teilt man die Punktwolke in zufällige Untermengen mit jeweils etwa \(m\) Punkten ein. Für jede berechnet man die konvexe Hülle, bspw. mit Andrews Algorithmus. Dann benutzt man Jarvis March, um die Hülle zu konstruieren, dabei muss man allerdings nicht mehr alle Punkte durchprobieren, sondern nur noch die Tangenten, die in der Animation mit grünen Strichen gekennzeichnet sind. Die Tangenten kann man für jede der \(k = \lceil \frac{n}{m} \rceil\) Sub-Hüllen effizient in \(\mathcal{O}(m)\) bestimmen. Dazu benutzt man einem Algorithmus, der an eine Binärsuche erinnert. Zusammen hat dies also eine Komplexität von \(\mathcal{O}((n+kh) \ln m)\).

Aber ich hatte \(\mathcal{O}(n \ln h)\) versprochen. Nun, um das zu erreichen, müssen wir einfach nur \(m \approx h\) wählen. Aber wie kommen wir an \(h\) bevor wir die Hülle berechnet haben? Der Trick ist, mit einem niedrigen \(m\) zu starten, dann nur \(m\) Schritte des Jarvis-Teils des Algorithmus durchzuführen und wenn die Hülle dann noch nicht fertig ist \(m\) zu erhöhen und es wieder von vorne zu beginnen. Damit dieser iterative Teil des Algorithmus nicht unsere Komplexität erhöht, muss \(m\) schnell genug wachsen, was in der Regel durch Quadrieren des alten Werten erreicht wird.

QuickHull

Zuletzt möchte ich hier noch QuickHull vorstellen, weil dieser Algorithmus meiner Meinung nach einen sehr hübschen rekursiven divide and conquer Ansatz verfolgt — ein bisschen wie QuickSort. In zwei Dimensionen starten wir mit dem Punkt ganz links \(A\) und ganz rechts \(B\). Dann finden wir den Punkt \(C\) der am weitesten entfernt ist von der Strecke \(\overline{AB}\) und links von der Strecke ist. Diesen Schritt wiederholen wir rekursiv auf den Strecken \(\overline{AC}\) und \(\overline{CB}\) (und \(\overline{BA}\) für die untere Hälfte.)

Mehr Dimensionen

Aber ich hatte Space Whales versprochen, also können wir uns nicht mit 2D zufrieden geben! Tatsächlich müssen wir schon beim Verallgemeinern auf 3D aufpassen. Schließlich konnten wir für 2D die konvexe Hülle als Sequenz von Punkten repräsentieren. Für höhere Dimensionen müssen wir sie allerdings als Menge von Facetten repräsentieren. Glücklicherweise tauchen für noch höhere Dimensionen dann keine weiteren Schwierigkeiten mehr auf — abgesehen von der Grundsätzlichen Schwierigkeit, dass höherdimensionale Gebilde deutlich größere Oberflächen haben und somit die konvexe Hülle aus deutlich mehr Facetten besteht, sodass die untere Schranke für die Komplexität für Dimension \(d\) durch \(\mathcal{O}(n^{\lfloor d / 2 \rfloor})\) gegeben ist.

Bevor ich hier QuickHull für \(d=3\) beschreibe, möchte ich darauf hinweisen, dass es die qhull Implementierung gibt, die sich bspw. auch um die subtilen numerischen Fehler kümmert, die sich bei sehr spitzen Winkeln einschleichen können.

Grundsätzlich bleibt das Vorgehen gleich: Wir starten mit einem \(d\)-dimensionalen Simplex, also für \(d=3\) mit einem Tetraeder, dessen Eckpunkte zur konvexen Hülle gehören. Dann führen wir für jede Facette den rekursiven Schritt durch: Finde den Punkt, der am weitesten vor der Facette (also außerhalb des Tetraeders) ist. Diesen Punkt nennt man Eye-Point. Denn es reicht jetzt im Gegensatz zum 2D Fall nicht mehr einfach neue Facetten aus den Rändern und dem neuen Punkt zu bilden. Stattdessen müssen wir alle Facetten, deren Vorderseite (also Außenseite) wir vom Eye-Point aus sehen können entfernen und neue Facetten mit dem Horizont und dem Eye-Point bilden. In der Animation unten sind der Eye-Point sowie die Facetten, die er sieht, rot dargestellt. Der Horizont ist mit schwarzen Strichen gekennzeichnet.

Wird dieser Schritt rekursiv auf alle neu hinzugefügten Facetten angewendet, resultiert die konvexe Hülle. Und genauso, wenn auch deutlich schwieriger darstellbar, funktioniert es auch für alle höheren Dimensionen.

Eine wichtige Anwendung für 3D konvexe Hüllen ist übrigens die Delaunay-Triangulation einer planaren Punktmenge. Die wiederum kann für eine effiziente Berechnung des Relative-Neighborhood-Graphs aus diesem Post genutzt werden.

Seit meinem ersten Eintrag über meinen Fraktal-tweetenden Bot @AFractalADay, habe ich selbigen noch um ein paar Fraktale erweitert, die ich hier kurz festhalten möchte. Der ganze Code ist auf Github.

Chaotic Maps

Eine Quadratic Map ist eine Rekursionsgleichung mit einem quadratischen Term, also beispielsweise

Das berühmteste Mitglied dieser Familie ist die Logistic-Map mit \(a_0=1, a_1=r, a_2=0\), die chaotisches Verhalten für \(3.56995 < r < 4\) zeigt. Aber leider ist sie nur eindimensional und ihr Attraktor deshalb nicht besonders hübsch.

Um visuell ansprechende Fraktale daraus zu erzeugen, brauchen wir also ein System aus zwei Rekursionsgleichungen, die wir als \(x\)- und \(y\)-Koordinaten betrachten können:

Jetzt haben wir 12 freie Parameter, die einen riesigen Parameterraum aufspannen, in dem etwa 1.6% aller Möglichkeiten chaotisches Verhalten mit einem seltsamen Attraktor zeigen.

Chaotische Differentialgleichungssysteme

Ein echter Klassiker ist das Differentialgleichungssystem, das die Chaostheorie begründet hat und nach dem der Schmetterlingseffekt benannt ist [1, 2]. Für bestimmte Paramtersätze verlaufen die Bahnkurven entlang eines seltsamen Attraktors, dessen fraktale Dimension \(\approx 2.06\) ist. Da der vollständige Attraktor somit in einer zweidimensionalen Projektion etwas langweilig aussieht, habe ich hier nur eine Trajektorie über kurze Zeit dargestellt.

Und es gibt eine ganze Menge weitere Differntialgleichungssysteme (und chaotic maps), die chaotische Attraktoren aufweisen. Deshalb zeige ich hier noch einen Rössler-Attraktor, der eine vereinfachte Version des Lorenz-Systems ist:

Und hier haben wir das Glück, dass auch seine Projektion sehr ansehnlich ist.

Ich persönlich frage mich, nun wie der Attraktor für das Doppelpendel aussieht. Es ist anscheinend kein Fraktal, aber es sieht dennoch ganz interessant aus:

Ising model

Das Ising Modell für Ferromagnetismus wird auch als Drosophila der statistischen Physik bezeichnet: Es ist ein einfaches Modell, dass einen Phasenübergang aufweist — Eisen verliert seine magnetischen Eigenschaften oberhalb der Curie-Temperatur.

Es besteht aus magnetischen Momenten, Spins, die gerne in die gleiche Richtung zeigen wie ihre Nachbarn, aber durch hohe Temperatur gestört werden. Oder etwas formaler: Die innere Energie \(U\) wird durch den Hamiltonian \(\mathcal{H} = - \sum_{<ij>} s_i s_j\) bestimmt, wobei \(s_i = \pm 1\), je nachdem ob der Spin up oder down ist und die Summe über benachbarte Spins läuft. Das System wird immer einen Zustand anstreben, der die freie Energie \(F=U-TS\) minimiert. Das kann entweder passieren, indem \(U\) möglichst klein ist oder die Entropie \(S\) möglichst hoch. Bei großen Werten der Temperatur \(T\) bekommt der Entropie-Term ein höheres Gewicht, sodass Zustände mit hoher Entropie, also zufälligen Spinausrichtungen, bevorzugt sind, bei niedrigen Temperaturen werden Konfigurationen mit niedriger innerer Energie bevorzugt, also solche in denen alle Spins in die selbe Richtung zeigen. Die Temperatur, bei der sich beide Terme die Waage halten, nennt man kritische Temperatur. Hier bilden sich Regionen von Spins, die in die gleiche Richtung zeigen, auf allen Größenskalen. Die fraktale Dimension dieser Regionen ist 187/96, was solche kritische Konfigurationen interessant anzusehen macht. Ich empfehle auf das folgende Bild zu klicken und etwas hineinzuzoomen.

Meine liebsten Probleme sind solche, die einfach scheinen aber sehr tief sind. Natürlich gehört das Problem des Handlungsreisenden dazu: Es ist einfach zu verstehen, dass der Müllmann bei jeder Mülltonne vorbei muss und dabei möglichst wenig Strecke fahren will. Gerade deshalb ist es das Paradebeispiel für NP-schwere Probleme (technisch gesehen ist nur seine Entscheidungs-Version „Gibt es eine Tour, die kürzer ist als \(X\)“ NP-schwer und nicht die typische Optimierungsversion: „Welche ist die kürzeste Tour“).

Aber fast noch besser gefällt mir das Problem der längsten aufsteigenden Teilfolge, oder auf englisch, longest increasing subsequence (LIS): Gegeben eine Folge von Zahlen \(S_i\), welche Teilfolge ist am längsten unter der Bedingung, dass die Zahlen aufsteigen.

Dieses Problem ist so einfach, dass es erstmals von Stanisław Ulam als Fingerübung beschrieben wurde und nach meinem Eindruck heutzutage als Übung für dynamische Programmierung in Universitäten verwendet wird. Wer weiß wie viele Bewerber vor einem Whiteboard ins Schwitzen geraten sind bei dem Versuch es aus dem Stegreif zu lösen.

Auf der anderen Seite ist es aber offenbar tief genug, dass man ganze Bücher darüber schreiben kann. Es zeigen sich überraschende Querverbindungen zu scheinbar unabhängigen Problemen. Denn die Länge \(L\) der LIS einer Permutation fluktuiert genauso wie der Abstand von der Mitte zum Rand eines Kaffeeflecks oder die größten Eigenwerte von Zufallsmatrizen.

Nun ist die Lösung dieses Problems nicht eindeutig: Es kann viele längste aufsteigende Teilfolgen geben. Tatsächlich wächst die Anzahl sogar exponentiell mit der Länge der ursprünglichen Sequenz.

Allerdings wurde bisher nie untersucht wie viele genau. Oftmals hört man, es sei nicht praktikabel alle durchzuzählen, da es exponentiell viele seien. Und wenn es darum ginge alle zu enumerieren, würde das stimmen. Aber wir wollen an dieser Stelle nur die Anzahl wissen, die wir mittels dynamischer Programmierung effizient bestimmen können. Die Idee ist, dass wir für jedes Element, das an Position \(x\) in einer LIS auftauchen kann, berechnen, wie viele aufsteigende Teilfolgen der Länge \(L-x\) mit diesem Element beginnen.

Besonders einfach geht das, wenn wir zuerst eine Datenstruktur aufbauen, die kodiert welche Elemente in einer LIS aufeinander folgen können. Dazu erweitern wir Patience Sort, und da dieser Algorithmus nach einem Kartenspiel benannt ist, werden wir es auch mit Karten visualisieren: Wir schreiben jedes Element unserer Sequenz auf eine Karte und legen die Karten auf einen Stapel, sodass das erste Element der Sequenz oben liegt. Dann nehmen wir Karten von oben ab und legen sie auf verschiedene Stapel. Die erste Karte legen wir auf den ersten, noch leeren Stapel. Die folgenden Karten legen wir auf den ersten Stapel, dessen oberstes Element größer ist als die aktuelle Karte und ansonsten machen wir einen neuen Stapel rechts davon auf. Jedes mal wenn wir eine Karte ablegen, lassen wir sie auf alle Karten, die aktuell auf dem Vorgängerstapel liegen und kleiner sind, zeigen — dies sind die Karten die in einer aufsteigenden längsten Teilfolge direkt vor ihr auftauchen können.

Am Ende haben wir \(L\) Stapel, wobei \(L\) die Länge der LIS ist, und wir können vom Stapel ganz rechts starten und den Pfeilen folgen, um eine LIS zusammenzubauen. Wenn wir nur an der Länge interessiert wären, müssten wir uns über den Inhalt der Stapel keine Gedanken machen und der Algorithmus ließe sich sehr kompakt darstellen:

fn lis_len<T: Ord>(seq: &[T]) -> usize {
    let mut stacks = Vec::new();
    for i in seq {
        let pos = stacks.binary_search(&i)
            .err()
            .expect("Encountered non-unique element in sequence!");
        if pos == stacks.len() {
            stacks.push(i);
        } else {
            stacks[pos] = i;
        }
    }
    stacks.len()
}

Aber wir wollen mehr, deshalb notieren wir uns im nächsten Schritt bei allen Karten des rechtesten Stapels wie viele aufsteigende Teilfolgen der Länge \(x=1\) mit ihnen starten, was trivialerweise je eine ist. Dann notieren wir bei allen Karten des Stapels links davon wie viele aufsteigenden Teilfolgen der Länge 2 mit ihnen anfangen. Das können wir berechnen, indem wir den Pfeilen rückwärts folgen und die Annotationen jeweils aufaddieren. Nachdem wir dies für alle Stapel wiederholt haben und den linkesten Stapel beschriftet haben, können wir alle Annotationen des linkesten Stapels aufaddieren, um die gesamte Anzahl LIS zu erhalten: hier \(7\).

Wie sich das ganze für längere Sequenzen aus unterschiedlichen Zufallsensembles im Detail verhält haben wir in einem Artikel veröffentlicht.