möchte­gern­geek

My favorite problems are those which seem simple but exhibit unexpected depth. A prime example is the Traveling Salesperson Problem: It is simple to understand that the garbage truck needs to collect every garbage container, while trying to take the shortest route.

But here, I want to talk about the problem of the longest increasing subsequence (LIS): For a given sequence of numbers, find the subsequence consisting of increasing numbers, which is longest.

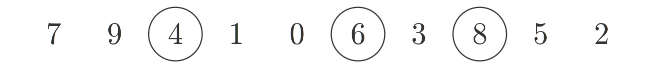
This problem is so simple that it was first studied almost as a placeholder by Stanisław Ulam in a book chapter describing the Monte Carlo method. And judging by the google results, it seems to be a common problem posed to university students. I am wondering how many job applicants were distressed when trying to solve it in front of a whiteboard.

However, apparently one can write whole books about this problem. It turns out that there are surprising connections to seemingly independent problems. For example, the length $$ of a LIS of a permutation fluctuates the same way as the distance from the center to the border of a coffee stain or the largest eigenvalues of random matrices.

The solution of this problem is not unique: A Sequence can contain multiple longest increasing subsequences. Indeed, their number grows exponentially with the length of the original sequence.

![Different longest increasing subsequences within the same sequence](/img/lis_alternatives.png]{: .invertable}

But up to now, there did not exist any results about the precise number of different LIS. A common sentiment is that counting all LIS was infeasible, since there are exponentially many. And that would be true if we would want to enumerate them. But since we only want to now the number, we can use dynamic programming to determine it efficiently. The basic idea is that we calculate for each element that can appear at position $$ in a LIS of how many increasing subsequences of length $$ it is the first element.

This becomes easy thanks to a datastructure encoding which elements can be subsequent in a LIS. For this we extend Patience Sort. Since the algorithm is called after a game of cards, it is adequate to describe it with cards: We write each element of our sequence on a card and sort the deck according to the sequence such that the first element is on top. Then we take cards from the top of the deck. We put the topmost card on the table opening a stack. We put the next card on the first stack whose top card is larger than it or open a new stack right of the currently rightmost stack. Each time we put a card on the table, we also add pointers to all cards of the stack left of the placed card which are smaller. These are the cards which could be its predecessor in a LIS.

In the end there are $$ stacks, where $$ is the length of the LIS. We can start from the rightmost stack, select an arbitrary element and follow the pointers to build a LIS. If we were only interested in the length, we could disregard all but the top card of every stack and could simply the algorithm:

fn lis_len<T: Ord>(seq: &[T]) -> usize {
    let mut stacks = Vec::new();
    for i in seq {
        let pos = stacks.binary_search(&i)
            .err()
            .expect("Encountered non-unique element in sequence!");
        if pos == stacks.len() {
            stacks.push(i);
        } else {
            stacks[pos] = i;
        }
    }
    stacks.len()
}

But we want more, therefore we annotate each card of the rightmost stack with the number of increasing subsequences of length $$ of which they are the first element, which is trivially 1 for each card. Then we continue with the stack left of it and annotate how many increasing subsequences of length 2 start with them. We can calculate this easily by following the pointers backwards and add up the annotations of all predecessor cards. After repeating this and annotating the leftmost stack, we can sum all annotations of the leftmost stack to get the total number of distinct LIS: here $$.

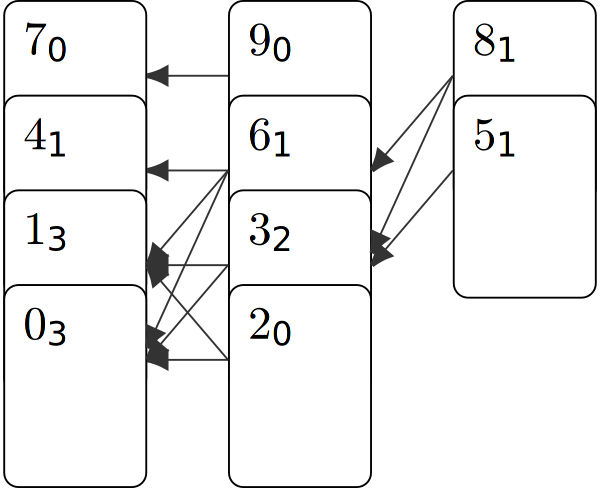
About the behavior for longer sequences from different random ensembles we published an article.