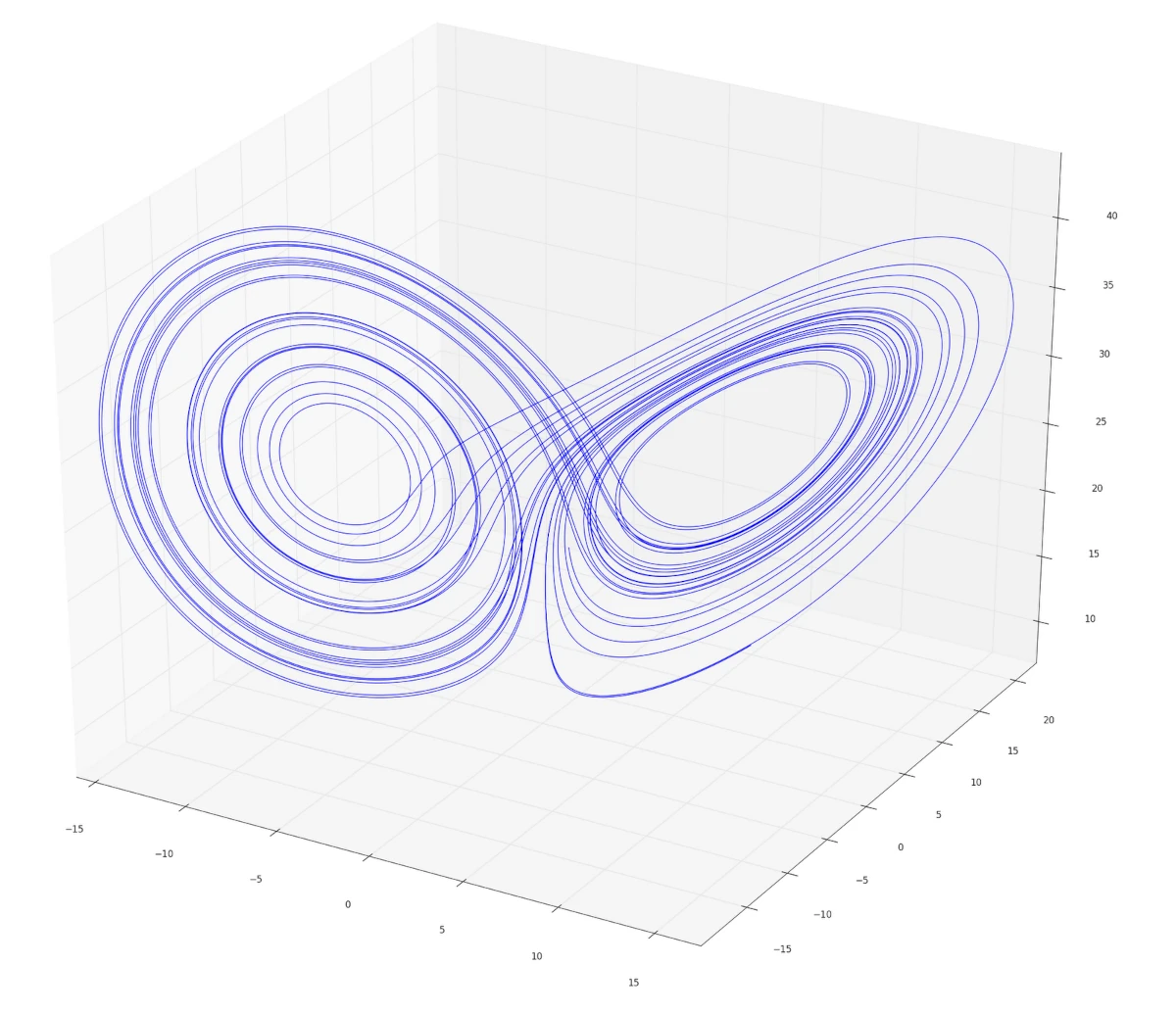
Schmetterlingseffekt
Differentialgleichungen numerisch zu lösen macht mehr Spaß, als man erwarten würde, wenn man es hört. Und sobald man den ersten Runge-Kutta-Algorithmus in einer kommerziellen Interpretersprache geschrieben hat, bemerkt man, dass dieses Skript doch recht lange braucht.
Für dieses Problem gibt es zwei Lösungen: Entweder wird man zum Guru und wendet irgendeine okkulte Matlab-Magie an, um das Programm schneller laufen zu lassen, oder man schreibt das Programm in einer schönen Sprache neu. In C zum Beispiel.
Ich habe mich für den einfachen Weg
entschieden und wenig überraschend eine Tempoverbesserung von Faktor
Warum ich den Titel „Schmetterlingseffekt“ gewählt habe? Naja, das Bild hier sieht ein wenig nach einem Schmetterling aus. Und tatsächlich wurde der Schmetterlingseffekt nach diesem Differentialgleichungssystem benannt — und nicht nach der Geschichte aus Jurassic Park.
Er bewegt in Peking die Flügel, und im Central Park gibt’s Regen statt Sonne.
— Dr. Ian Malcolm (1993)
Wie genau der Lorenzattraktor mit Chaos zusammenhängt, habe ich in diesem Post dargestellt.
Der Quellcode ist als Gist auf GitHub.