möchte­gern­geek

Meine liebsten Probleme sind solche, die einfach scheinen aber sehr tief sind. Natürlich gehört das Problem des Handlungsreisenden dazu: Es ist einfach zu verstehen, dass der Müllmann bei jeder Mülltonne vorbei muss und dabei möglichst wenig Strecke fahren will. Gerade deshalb ist es das Paradebeispiel für NP-schwere Probleme (technisch gesehen ist nur seine Entscheidungs-Version „Gibt es eine Tour, die kürzer ist als $X$“ NP-schwer und nicht die typische Optimierungsversion: „Welche ist die kürzeste Tour“).

Aber fast noch besser gefällt mir das Problem der längsten aufsteigenden Teilfolge, oder auf englisch, longest increasing subsequence (LIS): Gegeben eine Folge von Zahlen $S_i$, welche Teilfolge ist am längsten unter der Bedingung, dass die Zahlen aufsteigen.

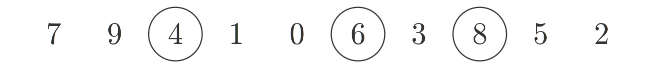
Dieses Problem ist so einfach, dass es erstmals von Stanisław Ulam als Fingerübung beschrieben wurde und nach meinem Eindruck heutzutage als Übung für dynamische Programmierung in Universitäten verwendet wird. Wer weiß wie viele Bewerber vor einem Whiteboard ins Schwitzen geraten sind bei dem Versuch es aus dem Stegreif zu lösen.

Auf der anderen Seite ist es aber offenbar tief genug, dass man ganze Bücher darüber schreiben kann. Es zeigen sich überraschende Querverbindungen zu scheinbar unabhängigen Problemen. Denn die Länge $$ der LIS einer Permutation fluktuiert genauso wie der Abstand von der Mitte zum Rand eines Kaffeeflecks oder die größten Eigenwerte von Zufallsmatrizen.

Nun ist die Lösung dieses Problems nicht eindeutig: Es kann viele längste aufsteigende Teilfolgen geben. Tatsächlich wächst die Anzahl sogar exponentiell mit der Länge der ursprünglichen Sequenz.

Allerdings wurde bisher nie untersucht wie viele genau. Oftmals hört man, es sei nicht praktikabel alle durchzuzählen, da es exponentiell viele seien. Und wenn es darum ginge alle zu enumerieren, würde das stimmen. Aber wir wollen an dieser Stelle nur die Anzahl wissen, die wir mittels dynamischer Programmierung effizient bestimmen können. Die Idee ist, dass wir für jedes Element, das an Position $$ in einer LIS auftauchen kann, berechnen, wie viele aufsteigende Teilfolgen der Länge $$ mit diesem Element beginnen.

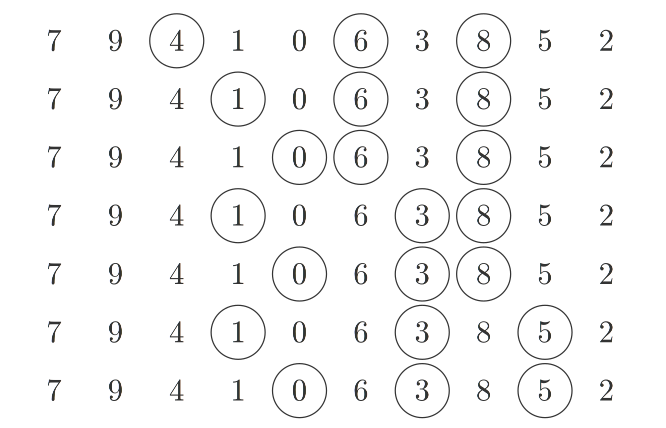
Besonders einfach geht das, wenn wir zuerst eine Datenstruktur aufbauen, die kodiert welche Elemente in einer LIS aufeinander folgen können. Dazu erweitern wir Patience Sort, und da dieser Algorithmus nach einem Kartenspiel benannt ist, werden wir es auch mit Karten visualisieren: Wir schreiben jedes Element unserer Sequenz auf eine Karte und legen die Karten auf einen Stapel, sodass das erste Element der Sequenz oben liegt. Dann nehmen wir Karten von oben ab und legen sie auf verschiedene Stapel. Die erste Karte legen wir auf den ersten, noch leeren Stapel. Die folgenden Karten legen wir auf den ersten Stapel, dessen oberstes Element größer ist als die aktuelle Karte und ansonsten machen wir einen neuen Stapel rechts davon auf. Jedes mal wenn wir eine Karte ablegen, lassen wir sie auf alle Karten, die aktuell auf dem Vorgängerstapel liegen und kleiner sind, zeigen — dies sind die Karten die in einer aufsteigenden längsten Teilfolge direkt vor ihr auftauchen können.

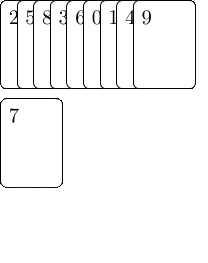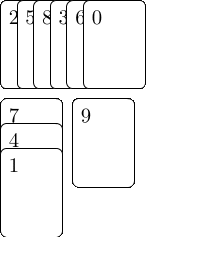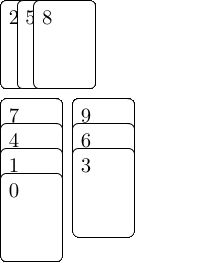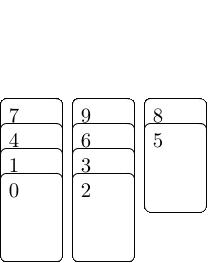
Am Ende haben wir $$ Stapel, wobei $$ die Länge der LIS ist, und wir können vom Stapel ganz rechts starten und den Pfeilen folgen, um eine LIS zusammenzubauen. Wenn wir nur an der Länge interessiert wären, müssten wir uns über den Inhalt der Stapel keine Gedanken machen und der Algorithmus ließe sich sehr kompakt darstellen:

fn lis_len<T: Ord>(seq: &[T]) -> usize {
    let mut stacks = Vec::new();
    for i in seq {
        let pos = stacks.binary_search(&i)
            .err()
            .expect("Encountered non-unique element in sequence!");
        if pos == stacks.len() {
            stacks.push(i);
        } else {
            stacks[pos] = i;
        }
    }
    stacks.len()
}

Aber wir wollen mehr, deshalb notieren wir uns im nächsten Schritt bei allen Karten des rechtesten Stapels wie viele aufsteigende Teilfolgen der Länge $$ mit ihnen starten, was trivialerweise je eine ist. Dann notieren wir bei allen Karten des Stapels links davon wie viele aufsteigenden Teilfolgen der Länge 2 mit ihnen anfangen. Das können wir berechnen, indem wir den Pfeilen rückwärts folgen und die Annotationen jeweils aufaddieren. Nachdem wir dies für alle Stapel wiederholt haben und den linkesten Stapel beschriftet haben, können wir alle Annotationen des linkesten Stapels aufaddieren, um die gesamte Anzahl LIS zu erhalten: hier $$.

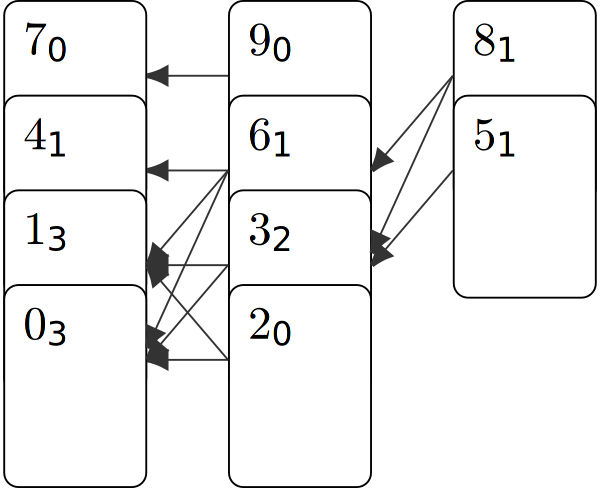
Wie sich das ganze für längere Sequenzen aus unterschiedlichen Zufallsensembles im Detail verhält haben wir in einem Artikel veröffentlicht.