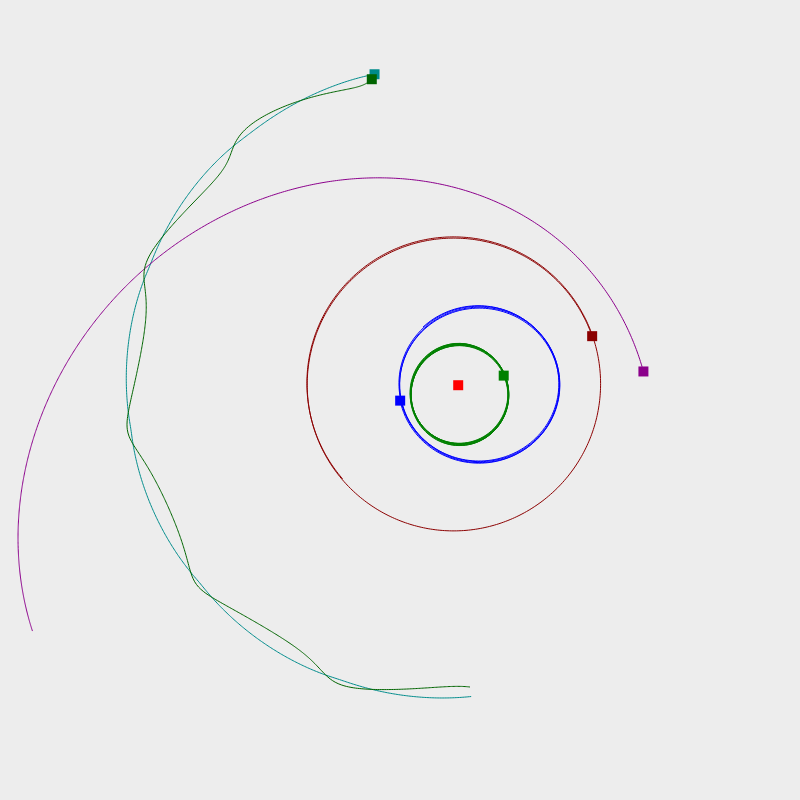
TSPview
Das Problem des Handlungsreisenden ist es, die kürzeste Rundtour zu planen, sodass man alle Städte besucht. Es ist eines der berühmtesten Optimierungsprobleme und gehört zur Klasse NP-hard.
Es gibt also (bis jetzt) keine effiziente Möglichkeit zur Lösung. Allerdings gibt es Näherungen, untere Schranken und unzählige Heuristiken.
Die einfachsten dieser Heuristiken habe ich in einem kleinen Programm TSPview implementiert, mitsamt Visualisierung. Der Quellcode ist auf GitHub zu finden.
Algorithmen
Hier folgt eine kurze Beschreibung der verwendeten Algorithmen und jeweils ein Bild, welche Lösung die Methode auf einer berühmten Instanz des TSP findet.
 Das sind 42 Hauptstädte der Vereinigten Staaten von Amerika und Washington, DC (Hawaii und
Alaska, sowie einige Staaten an der Ostküste, die das Problem nicht schwieriger
machen, fehlen). Dieses Problem war das erste größere, das 1956 beweisbar
optimal gelöst wurde.
Das sind 42 Hauptstädte der Vereinigten Staaten von Amerika und Washington, DC (Hawaii und
Alaska, sowie einige Staaten an der Ostküste, die das Problem nicht schwieriger
machen, fehlen). Dieses Problem war das erste größere, das 1956 beweisbar
optimal gelöst wurde.
Nearest Neighbor
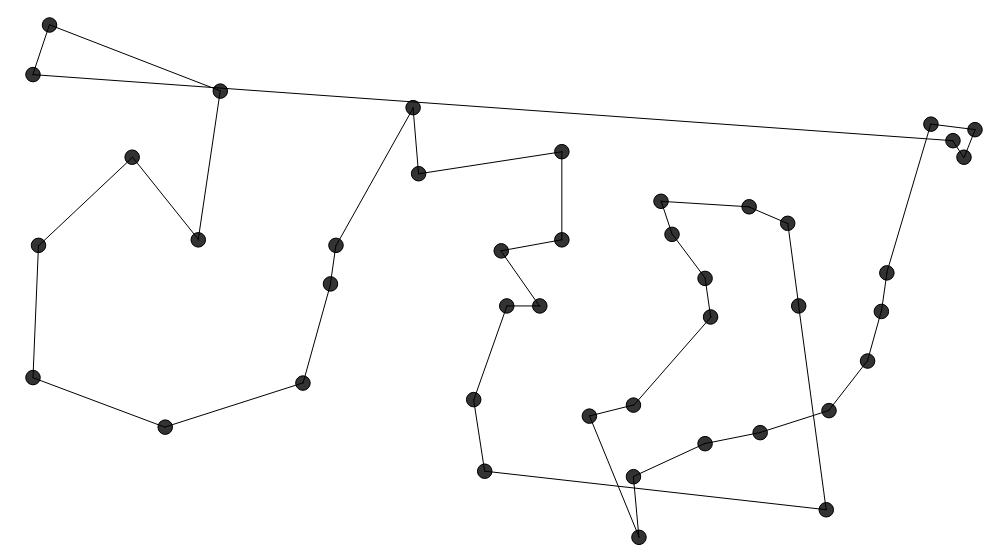 Die Nearest Neighbor Heuristik (
Die Nearest Neighbor Heuristik (
Greedy
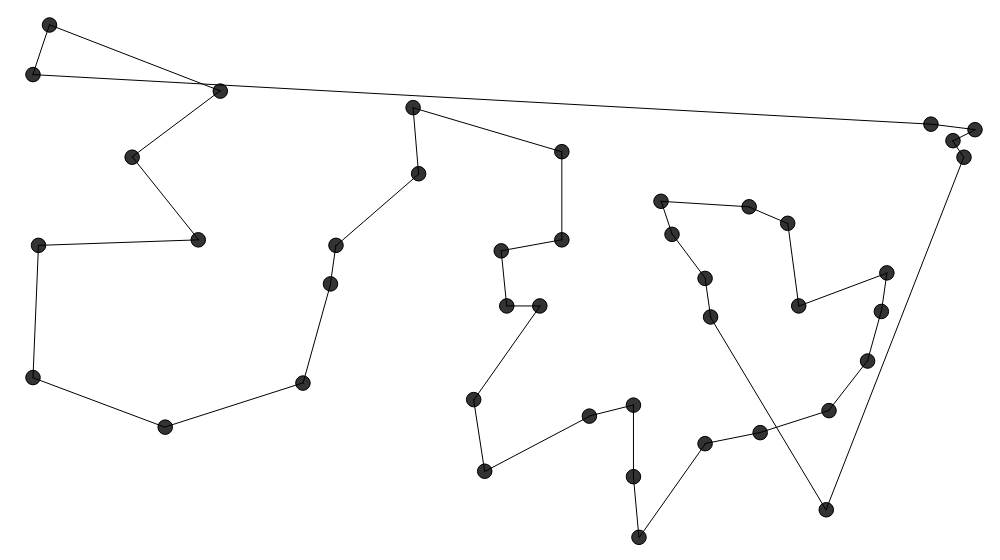 Diese Heuristik (
Diese Heuristik (
Farthest Insertion
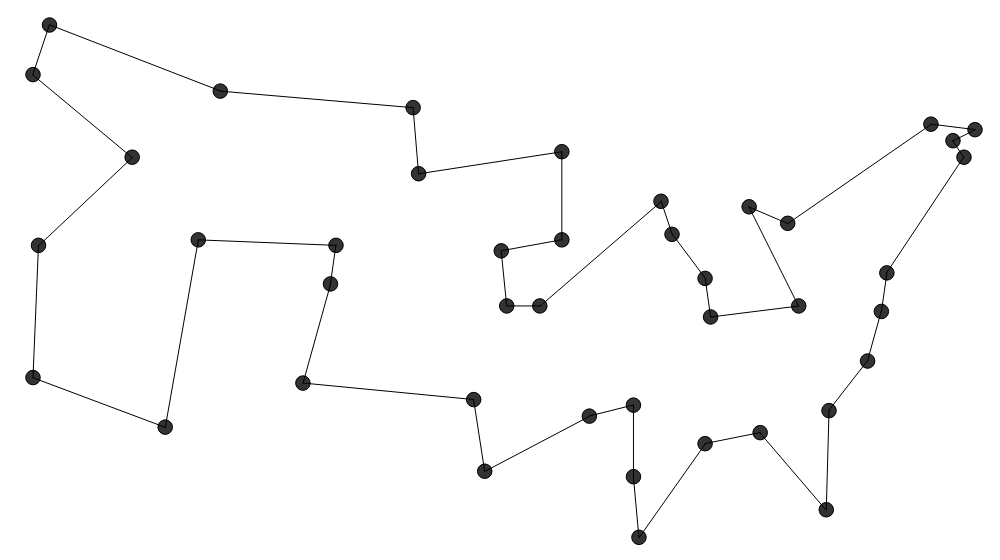 Farthest Insertion (
Farthest Insertion (
Two-Opt
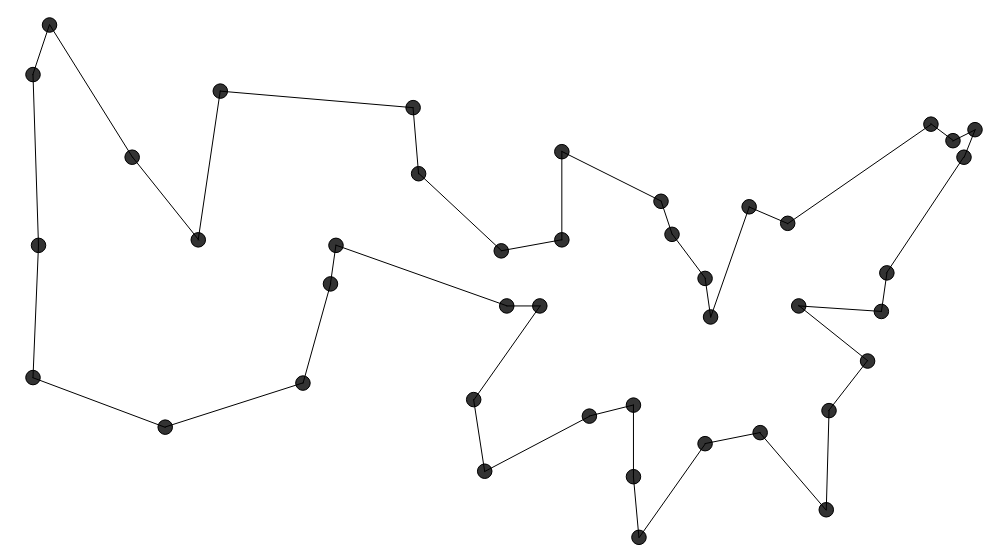 Two-Opt beginnt mit einer beliebigen Tour, die bspw. durch eine der obigen
Heuristken erstellt wurde und verbessert sie, indem sie zwei Verbindungen nimmt
und die Endpunkte über Kreuz austauscht, wenn die Tour dadurch verbunden bleibt
und kürzer wird.
Two-Opt beginnt mit einer beliebigen Tour, die bspw. durch eine der obigen
Heuristken erstellt wurde und verbessert sie, indem sie zwei Verbindungen nimmt
und die Endpunkte über Kreuz austauscht, wenn die Tour dadurch verbunden bleibt
und kürzer wird.
Lineare Programmierung mit „Subtour Elimination Cuts“
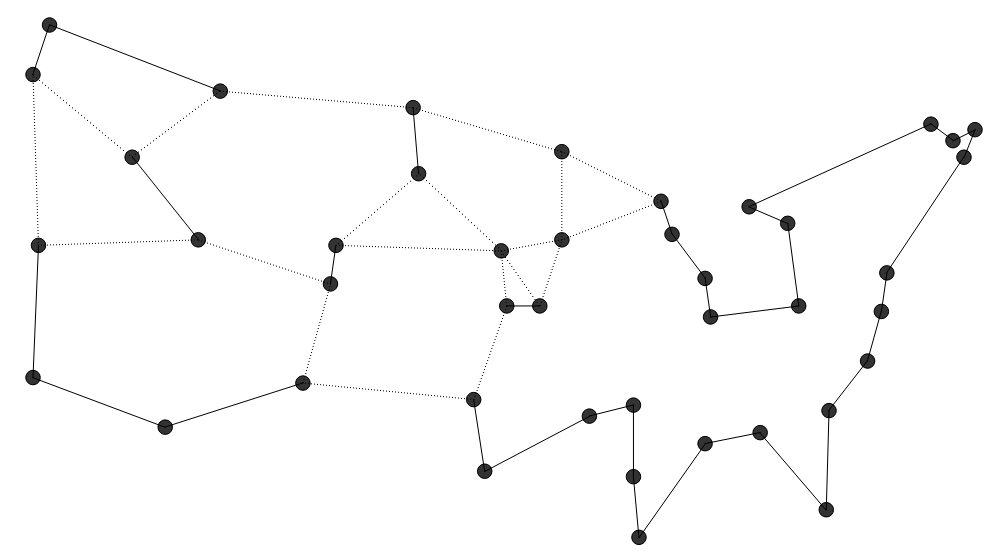 Lineare Programmierung (LP) zu erklären, würde diesen Artikel sprengen. Aber diese Methode liefert
untere Schranken für die Tourlänge und kann somit benutzt werden, um die
Qualität einer heuristischen Lösung abzuschätzen. Falls man die optimale
Lösung durch lineare Programmierung findet, erkennt man sie auch sofort als optimal.
Lineare Programmierung (LP) zu erklären, würde diesen Artikel sprengen. Aber diese Methode liefert
untere Schranken für die Tourlänge und kann somit benutzt werden, um die
Qualität einer heuristischen Lösung abzuschätzen. Falls man die optimale
Lösung durch lineare Programmierung findet, erkennt man sie auch sofort als optimal.
Für weitere Details, kann ich auf einen arXiv Artikel von mir verweisen.
Concorde
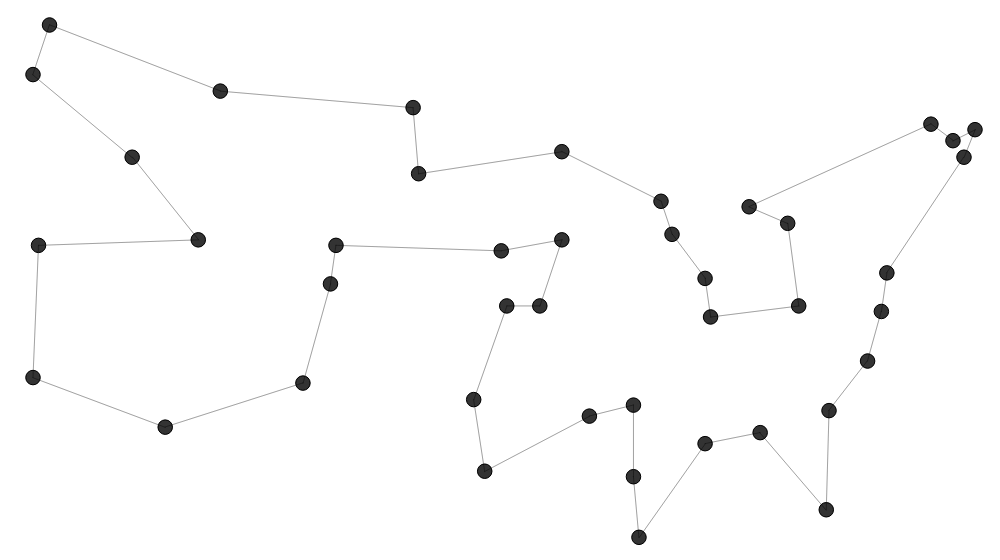 Concorde
ist der „State of the Art“ Solver für das Problem des Handlungsreisenden
und löst problemlos Instanzen mit mehr als 1000 Städten.
Intern benutzt es zwar eine Menge Heuristiken, allerdings auch lineare
Programmierung, um nachzuweisen, dass die gefundene Lösung optimal ist.
Concorde
ist der „State of the Art“ Solver für das Problem des Handlungsreisenden
und löst problemlos Instanzen mit mehr als 1000 Städten.
Intern benutzt es zwar eine Menge Heuristiken, allerdings auch lineare
Programmierung, um nachzuweisen, dass die gefundene Lösung optimal ist.
Technische Details
TSPview ist ein Python3 Programm, das zur Darstellung PyQt5 benutzt, das sich
per pip3 install PyQt5 einfach installieren lässt.
Darüber hinaus enthält es eine optionale Abhängigkeit zu CPLEX, einem kommerziellen LP solver.
boost::python
Da das Hauptprogramm in Python geschrieben ist, aber der LP-Teil in C++, braucht man eine Möglichkeit der Kommunikation. Glücklicherweise gibt es mit boost::python eine Möglichkeit C++ Klassen in Python als Python-Klassen zu benutzen.
Um beispielsweise die C++ Klasse MyClass, deren Konstruktor einen Integer und
eine Python-Liste entgegen nehmen soll, in Python benutzen und myMethod
aufrufen zu können, reicht folgender Code:
#include <boost/python.hpp>
namespace py = boost::python;
// implement MyClass
BOOST_PYTHON_MODULE(MyClass)
{
py::class_<MyClass>("MyClass", py::init<int, py::list>())
.def("myMethod", &MyClass::myMethod)
;
}