DGLshow
Nachdem ich so vielen Differenzialgleichungssystemen [1, 2, 3, 4] begegnet bin, die sich nicht analytisch lösen lassen, habe ich mir ein Programm zur numerischen Lösung und Visualisierung derselben geschrieben.
Die grundlegende Idee zur numerischen Lösung von Differentialgleichungen ist es, die Zeit in diskreten Schritten $\tau$ vergehen zu lassen. Nach jedem Schritt wird der Zustand so geändert, als ob sich während des Zeitschrittes nichts geändert hätte und die „Kräfte“ werden entsprechend der Bewegungsgleichungen neu berechnet. Für infinitesimal kleine $\tau \to \mathrm{d}t$ ist diese Methode schließlich exakt.
Im einfachsten Fall, dem Euler Verfahren, sähe das für ein einfaches Fadenpendel nach $k$ Zeitschritten so aus \begin{align} \ddot\vartheta_{k+1} &= - mgl \sin(\vartheta_k)\ \dot\vartheta_{k+1} &= \tau \ddot\vartheta_{k} + \dot\vartheta_{k}\ \vartheta_{k+1} &= \tau \dot\vartheta_{k} + \vartheta_{k} \end{align} Unglücklicherweise hat dieses Verfahren ernsthafte Probleme mit der Energieerhaltung und braucht sehr kleine $\tau$ für brauchbare Ergebnisse. Es gibt deutlich ausgefeiltere Methoden, wie den klassischen Runge-Kutta Algorithmus. Es gibt Methoden, den Zeitschritt $\tau$ während der Simulation adaptiv anzupassen, um nur wenig Rechenaufwand in den wenig fehleranfälligen Phasen zu verbringen. Es gibt spezialisierte Methoden, die sehr gut für bestimmte Bewegungsgleichungen funktionieren, wie Velocity-Verlet, der oft für Molekulardynamiksimulationen eingesetzt wird.
Chaotische Systeme haben in der Regel etwas kompliziertere Bewegungsgleichungen. Das oben abgebildete Doppelpendel etwa wird, wie ich in einem anderen Post beschrieben habe durch folgendes Ungetüm beschrieben.
\begin{align} \ddot\theta_1 &= \frac{m_2 \cos(\theta_1 - \theta_2) (l_1 \sin(\theta_1 - \theta_2) \dot\theta_1^2 - g \sin(\theta_2)) + m_2 l_2 \sin(\theta_1 - \theta_2) \dot\theta_2^2 + (m_1 + m_2) g \sin(\theta_1)}{m_2 l_1 \cos^2(\theta_1 - \theta_2) - (m_1+m_2) l_1} \ \ddot\theta_2 &= \frac{m_2 l_2 \cos(\theta_1 - \theta_2) \sin(\theta_1 - \theta_2) \dot\theta_2^2 + (m_1+m_2) l_1 \sin(\theta_1 - \theta_2) \dot\theta_1^2 + (m_1+m_2) g \cos(\theta_1 - \theta_2) \sin(\theta_1) - (m_1+m_2) g \sin(\theta_2)}{(m_1+m_2) l_2 - m_2 l_2 \cos^2(\theta_1 - \theta_2)} \end{align}
Anfangs empfiehlt es sich also etwas einfacheres und vertrauteres zu lösen, wie den Lorenz-Attraktor \begin{align} \dot{X} &= a(Y - X) \ \dot{Y} &= X(b - Z) - Y \ \dot{Z} &= XY - cZ \ \end{align}
Oder das Dreikörperproblem \begin{align} \ddot{\vec{x}_1} &= -\frac{Gm_2}{\left(x_1 - x_2\right)^3} (\vec{x}_1 - \vec{x}_2) - \frac{Gm_3}{\left(x_1 - x_3\right)^3} (\vec{x}_1 - \vec{x}_3)\ \ddot{\vec{x}_2} &= -\frac{Gm_1}{\left(x_2 - x_1\right)^3} (\vec{x}_2 - \vec{x}_1) - \frac{Gm_3}{\left(x_2 - x_3\right)^3} (\vec{x}_2 - \vec{x}_3)\ \ddot{\vec{x}_3} &= -\frac{Gm_1}{\left(x_3 - x_1\right)^3} (\vec{x}_3 - \vec{x}_1) - \frac{Gm_2}{\left(x_3 - x_2\right)^3} (\vec{x}_3 - \vec{x}_2)\ \end{align}
Da man das 3-Körperproblem trivial auf ein $N$-Körperproblem erweitern kann, habe ich hier ein „Sonnensystem“ bzw. Bohrsches „Atom“-modell simuliert.
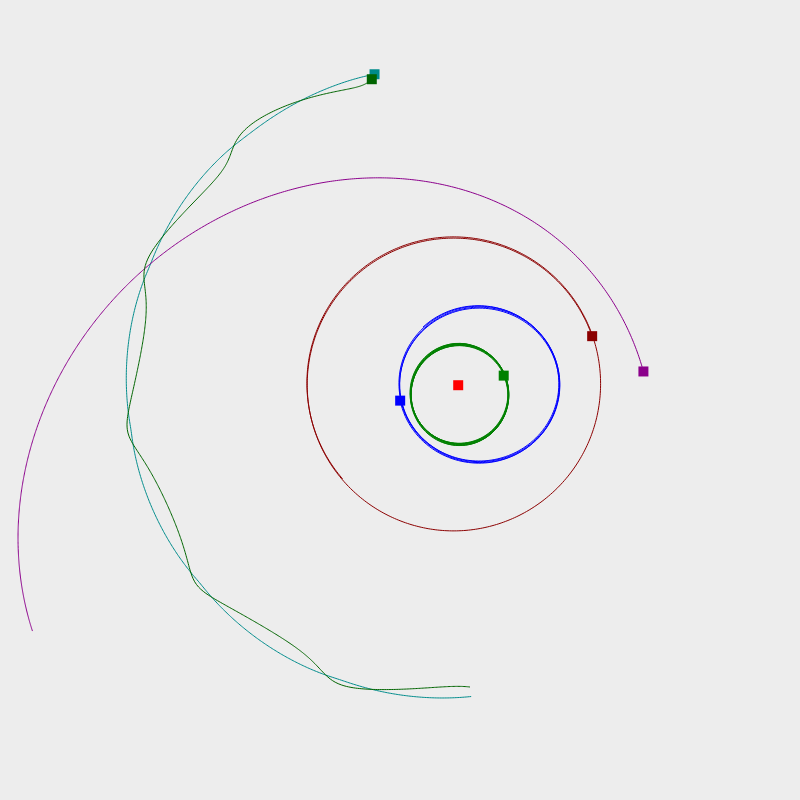
Um die obigen (bewegten) Bilder zu erzeugen und um ein bewegtes Doppelpendel für meinen Schreibtisch zu haben, — wennauch nur auf einem Bildschirm — habe ich in C++ einen adaptiven Runge-Kutta-4 Löser geschrieben, der mit den Qt Zeichenprimitiven animiert wird.
Auch wenn der Code nicht sehr aufgeräumt ist und Startwerte im Quellcode angepasst werden müssen, sind die Quellen auf GitHub: github.com/surt91/DGLshow.