Perfect Snake
Ich habe auf diesem Blog schon über eine Reihe von Snake Clonen [1, 2, 3, 4, 5] geschrieben, die zum Teil auch Autopilot-Strategien hatten [6, 7]. Die Autopiloten waren zwar meist interessant anzusehen — vor allem bei hohen Geschwindigkeiten — aber bei weitem nicht perfekt.
Auch wenn der Titel etwas zu viel verspricht, schafft es dieser Autopilot (zumindest manchmal) perfekte Spiele zu spielen.

Und falls dieses gif nicht überzeugt, kann man den Autopiloten online — dank TensorFlow.js — direkt im Browser ausprobieren auf snake.schawe.me.
Aber was steckt dahinter?
Neuronale Netze
Wenn man nicht clever genug ist, eine direkte Lösung für ein Problem zu finden, kann man versuchen ein neuronales Netz auf die Lösung des Problems zu trainieren. Vor einigen Jahren hat ein Artikel, in dem ein neuronales Netz trainiert wurde alte Atari-Spiele zu spielen, für mediale Aufmerksamkeit gesorgt. Und die gleiche Idee des Reinforcement Learning werde ich hier (nicht als erster [8, 9]) auf Snake anwenden.
Die grundlegende Idee von Reinforcement Learning ist relativ einsichtig: Wir belohnen das Modell für gute Entscheidungen, sodass es lernt mehr gute Entscheidungen zu treffen. In unserem Fall werden gute Entscheidungen dadurch definiert, dass sie zu einer hohen Punktzahl, also Länge der Schlange am Spielende, führen.
Glücklicherweise können wir auf die Literatur zurückgreifen, wie wir diese grundsätzliche Idee umsetzen können. Das Modell, für das ich mich entschieden habe, ist ein Actor-Critic Ansatz. Dabei nutze ich ein neuronales Netz, das als Input den aktuellen Zustand des Spielfeldes bekommt — wie genau dieser Zustand aussieht, diskutieren wir weiter unten. Dann geht es durch ein paar Schichten und endet in zwei „Köpfen“. Einer ist der Actor, mit drei Output-Neuronen, die für „nach links“, „nach rechts“ und „geradeaus weiter“ stehen. Der andere ist der Critic, der ein Output-Neuron hat, das abschätzt wie lang die Schlange, ausgehend von der aktuellen Situation, noch werden kann — also wie gut die aktuelle Situation ist.
Das Training läuft dann so ab, dass ein ganzes Spiel gespielt wird, folgend den Vorschlägen des Actors mit etwas rauschen, um neue Strategien zu erkunden. Sobald es beendet ist, weil die Schlange sich oder eine Wand gebissen hat, wird der Critic mit allen Zuständen des Spielverlaufs darauf trainiert, Schätzungen abzugeben, die möglichst gut zu der tatsächlich erreichten Länge am Spielende passen. Außerdem wird der Actor darauf trainiert gute Entscheidungen zu treffen, indem zu den Zuständen des Spielverlaufs andere Entscheidungen getroffen werden und die Bewertung des Critic der resultierenden Situationen als Qualität der Entscheidung genutzt wird. Actor und Critic helfen sich also gegenseitig besser zu werden. Der gemeinsame Teil des neuronalen Netzes sollte im Idealfall nach genügend gespielten Spielen dabei ein „Verständnis“ für Snake entwickeln. Genial!
Technische Nebensächlichkeiten
Meine Implementierung benutzt die Python Bibliotheken Keras und Tensorflow zum Training und multiJSnake als Environment. Wir steuern also einen Java-Prozess, um unser neuronales Netz in Python zu trainieren. Diese Entscheidung ist etwas unorthodox, aber bot Potential für einen Blogpost auf dem Blog meines Arbeitgebers.
Wir können das Environment getrost als Black-Box betrachten, die dafür sorgt, dass die Regeln von Snake befolgt werden.
Lokale Informationen
Eine der wichtigsten Entscheidungen ist nun, wie der Input in das Modell aussieht. Die einfachste Variante, die sich auch gut zum Testen eignet, ist die lokale Information rund um den Kopf der Schlange: Drei Neuronen, die jeweils 1 oder 0 sind, wenn das Feld links, rechts und geradeaus vom Kopf belegt sind (und acht weitere für etwas mehr Weitsicht auf die Diagonalen und übernächste Felder vorne, rechts, links und diesmal auch zurück). Damit die Schlange auch das Futter finden kann, fügen wir noch 4 weitere Neuronen hinzu, die per 1 oder 0 anzeigen, ob das Futter in, rechts, links oder entgegengesetzt der Bewegungsrichtung der Schlange ist.
Mit diesem Input füttern wir eine einzelne vollvernetzte Schicht, hinter der wir direkt die Actor und Critic Köpfe anschließen.
Das reicht aus, damit die Schlange nach ein paar tausend Trainingsspielen zielstrebig auf das Futter zusteuert und sich selbst ausweicht. Allerdings reicht es noch nicht, um zu verhindern, dass sie sich selbst in Schlaufen fängt. Da war der Autopilot von rsnake besser.
Globale Informationen
Um der Schlange eine Chance zu geben zu erkennen, dass sie sich gerade selbst fängt,
sollte man ihr erlauben das ganze Spielfeld zu sehen — schließlich sehen menschliche
Spieler auch das ganze Spielfeld. Bei einem
- der Kopf: nur an der Position des Kopfes ist eine 1, der Rest ist 0
- der Körper: die Positionen an denen sich der Körper befindet zeigen wie viele Zeitschritte der Körper noch an dieser Position sein wird
- das Futter: nur an der Position des Futters ist eine 1, der Rest ist 0
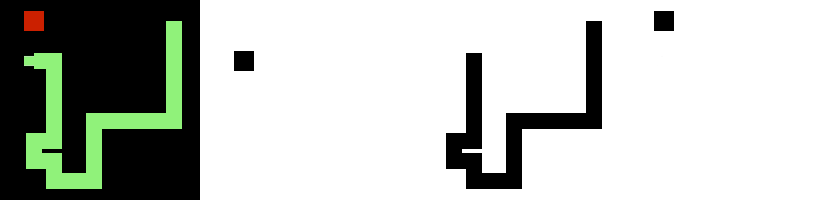
Dies ist auch kein unfairer Vorteil, schließlich sehen menschliche Spieler das Bild auch mit drei Farbkanälen.
Und damit die Schlange nicht auch noch lernen muss was rechts und links bedeutet, geben wir dem Actor 4 Outputs, die für Norden, Osten, Süden und Westen stehen.
Dieses Modell-Layout verdient es dann schon eher als Deep Learning bezeichnet zu werden. Weitere Modell-Parameter, können auf github.com/surt91/multiJSnake nachgeschlagen werden.
Nach einigen zehntausend Trainingsspielen funktioniert dieses Modell dann
tatsächlich gut genug, um regelmäßig perfekte Spiele auf einem