Vor einiger Zeit habe ich ein Programm geschrieben, das verschiedene Typen von
Fraktalen generiert. Da viele Methoden Fraktale zu generieren relativ einfach
zu parallelisieren sind und großen Bedarf an Rechenkraft haben, habe ich mich
entschieden es in Rust zu implementieren. Bei Interesse kann das
Programm von Github bezogen werden.
Da Fraktale nett anzuschauen sind, ist dieser Beitrag voller hochaufgelöster
Bilder. Damit diese Seite dennoch flüssig geladen wird — auch bei langsamen
Verbindungen, habe ich extra für diesen Eintrag in die
Technik dieses Blogs eingegriffen.
Außerdem gibt es @AFractalADay auf
Twitter, der täglich ein zufälliges Fraktal tweetet.
Escape Time
Die erste Klasse von Fraktalen, die ich hier zeigen möchte, wird definiert durch
das Konvergenzverhalten des wiederholten Anwendens einer Funktion. Was genau
dieser Satz bedeutet, lässt sich am besten an einem Beispiel erklären.
Mandelbrot-Menge
Das vermutlich bekannteste Fraktal ist das Apfelmännchen, das die
Mandelbrotmenge visualisiert. Das ist die Menge der komplexen Zahlen
die nicht konvergieren, wenn die Funktion
wiederholt angewendet wird. Also wenn die Folge
gegen einen endlichen Wert strebt.
Wenn man jeden Punkt auf der komplexen Ebene entsprechend des Konvergenzverhaltens
bezüglich dieser Folge einfärbt — schwarz wenn es konvergiert, blau für langsame
Divergenz, rot für schnelle Divergenz — erhält man ein solches Bild:

Dies ist ein Zoom auf den Rand des Apfelmännchens. Tatsächlich ist die
Mandelbrotmenge kein Fraktal im eigentlichen Sinne, da seine fraktale Dimension
2 ist — der schwarze Bereich füllt eine Fläche.
Es einfach möglich dieses Fraktal zu rastern und dabei jeden Pixel parallel zu
berechnen. Eine naive Implementierung könnte wie folgt aussehen.
// convenient iterators
#[macro_use] extern crate itertools;
use itertools::Itertools;
// parallelism
extern crate rayon;
use rayon::prelude::*;
// complex numbers
extern crate num;
use num::complex::Complex;
fn raster(resolution: (u32, u32)) -> Vec<u64> {
let (x, y) = resolution;
// generate the points, we want to raster
let pixels: Vec<(u32, u32)> = iproduct!(0..y, 0..x).collect();
// start a parallel iterator on the points ...
pixels.par_iter()
.map(|&(j, i)| {
// ... mapping every point ...
let z = map_to_cplx_plane(i, j);
// ... to the number of iterations needed to diverge
time_to_diverge(z)
})
.collect()
}
fn map_to_cplx_plane(x: u32, y u32) -> Complex<f64> {
// TODO: here we need to get the offset and scale somehow
let x = (x-x_offset) as f64 * x_scale;
let y = (y-y_offset) as f64 * y_scale;
Complex<f64> {re: x, im: y}
}
fn time_to_diverge(mut state: Complex<f64>) -> u64 {
// threshold is 2^2, since we compare to the square of the norm
// as soon as the norm is >= 2 it is sure to diverge
let threshold = 4.;
// abort after 1000 iterations
let max_count = 1000;
let c = state;
let mut ctr = 0u64;
while {
state = state * state + c;
ctr += 1;
state.norm_sqr() < threshold && ctr < max_count
} {}
ctr
}
Julia-Mengen
Nahe verwandt sind die Julia-Mengen. Hier benutzt man die gleiche Funktion ,
allerdings färbt man jeden Punkt entsprechend seines Konvergenzverhaltens
bei einem festen Parameter .

Tatsächlich ist jede beliebige Funktion erlaubt und nicht nur die oben erwähnte
quadratische. Mit unkonventioneller Zuordnung von Farben zu Divergenzzeiten
ergibt sich mit dieses Bild:

Newton-Fraktal
Das Newton-Verfahren zur Findung von Nullstellen
startet an einem beliebigen Punkt auf einer Kurve, und berechnet die Nullstelle
der Tangente an diesem Punkt. Mit der Tangente dieses Punktes wird genauso
verfahren. Dabei sollten sich die so erhaltenen Punkte immer dichter einer
Nullstelle nähern. Bei einer komplexen Funktion können wir dies für jeden
Startpunkt iterieren. Jeder Punkt wird gegen eine Nullstelle konvergieren, der
wir eine Farbe zuordnen und den Punkt mit dieser Farbe einfärben. Wenn wir die
Sättigung davon abhängig machen, wie schnell die Konvergenz ist, sieht das
Ergebnis für so aus.

Chaos Game
Eine große Klasse von Fraktalen lässt sich mit dem Chaos Game erzeugen. Man
benutzt dazu mindestens zwei Abbildungen und , die jeweils einen
Punkt auf einen anderen Punkt abbilden. Man wählt einen Punkt zum Starten,
bildet ihn mit einer Zufälligen der beiden Abbildungen ab, zeichnet den
resultierenden Punkt ein und wiederholt dies sehr oft.
Dieser Algorithmus ist inherent sequenziell, allerdings kann man parallel an
vielen verschiedenen Punkten starten und die Ergebnisse dieser unabhängigen
Markovketten in einem Bild zusammenführen.
In Rust könnte der entsprechende Codeschnipsel so aussehen:
extern crate num_cpus;
use std::thread;
use std::sync::mpsc::channel;
let cpus = num_cpus::get();
// create a transmitter, receiver pair
let (tx, rx) = channel();
for _ in 0..cpus {
// clone a transmitter for each thread
let tx = tx.clone();
// generator yielding the points from the chaos game
// using a random seed
let sampler = get_sampler();
// we need some histogram implementation
let mut hist = Histogram::new();
thread::spawn(move || {
// feed the samples into the histogram
hist.feed(sampler.take(iterations_per_task));
// send the finished histogram to the receiver
tx.send(hist).unwrap();
});
}
// collect all parallel computed histograms into main_hist
let mut main_hist = Histogram::new();
for _ in 0..cpus {
let h = rx.recv().unwrap();
main_hist.merge(&h);
}
Sierpinski-Dreieck und Barnsley-Farn
Mit dieser Methode kann man alte Bekannte wie das Sierpinski-Dreieck erzeugen.

Dazu benötigt man die drei affinen Transformationen, die man alle mit gleicher
Wahrscheinlichkeit auswählt:
$$\begin{align}
f_1(\vec z) &=\begin{pmatrix}
-1/4 & \sqrt 3 / 4 \
-\sqrt 3 / 4 & -1/4
\end{pmatrix}
\cdot
+
\
f_2(\vec z) &=\begin{pmatrix}
1/2 & 0 \
0 & 1/2
\end{pmatrix}
\cdot
+
\
f_3(\vec z) &=\begin{pmatrix}
-1/4 & -\sqrt 3 / 4 \
\sqrt 3 / 4 & 1/4
\end{pmatrix}
\cdot
+
\end{align}$$
Ein anderes berühmtes Beispiel ist der Barnsley-Farn. Um ihn zu erzeugen, benutzt
man die folgenden vier affinen Abbildungen, die man mit den Wahrscheinlichkeiten
verwendet:
$$\begin{align}
f_1(z) &=\
f_2(z) &=\begin{pmatrix}
0.85 & 0.04 \
0 & -0.04
\end{pmatrix}
\cdot
+
\
f_3(z) &=\begin{pmatrix}
0.2 & -0.26 \
0 & 0.23
\end{pmatrix}
\cdot
+
\
f_4(z) &=\begin{pmatrix}
-0.15 & 0.28 \
0 & 0.26
\end{pmatrix}
\cdot
+
\ \end{align}$$
Als Ergebnis erhält man diesen Farn.

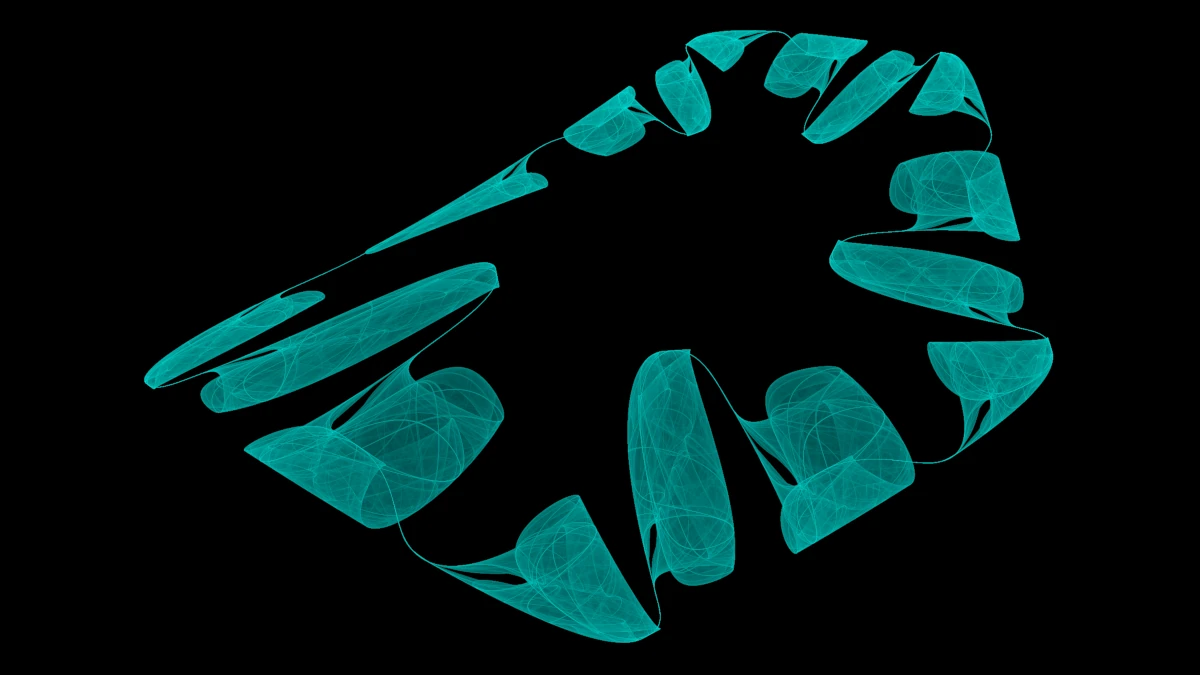
Fractal Flame
Fractal Flame ist der Name einer Klasse
von Zufallsfraktalen, die nach dem gleichen Muster wie oben aus einer Reihe
affiner Transformationen bestehen. Zusätzlich können die affinen
Transformationen mit einer nichtlinearen Variation erweitert werden,
sodass (oder Linearkombinationen dieser Variationen).
Zur Visualisierung werden die Punkte nicht direkt gezeichnet, sondern in ein
Histogramm eingetragen, aus dem die Farbintensitäten typischerweise
logarithmisch berechnet werden.

Hier wird jedem ein Farbton zugeordnet. Die Farbe eines Punktes ist eine
Mischung dieser Farben, die widerspiegelt, wie oft eine Abbildung genutzt wurde,
um an diesen Punkt zu gelangen.
Interessanterweise sind diese Systeme anscheinend sehr anfällig für schlechte
Zufallszahlen, was sich in „Löchern“ in den ansonsten glatten Flächen bemerkbar macht.
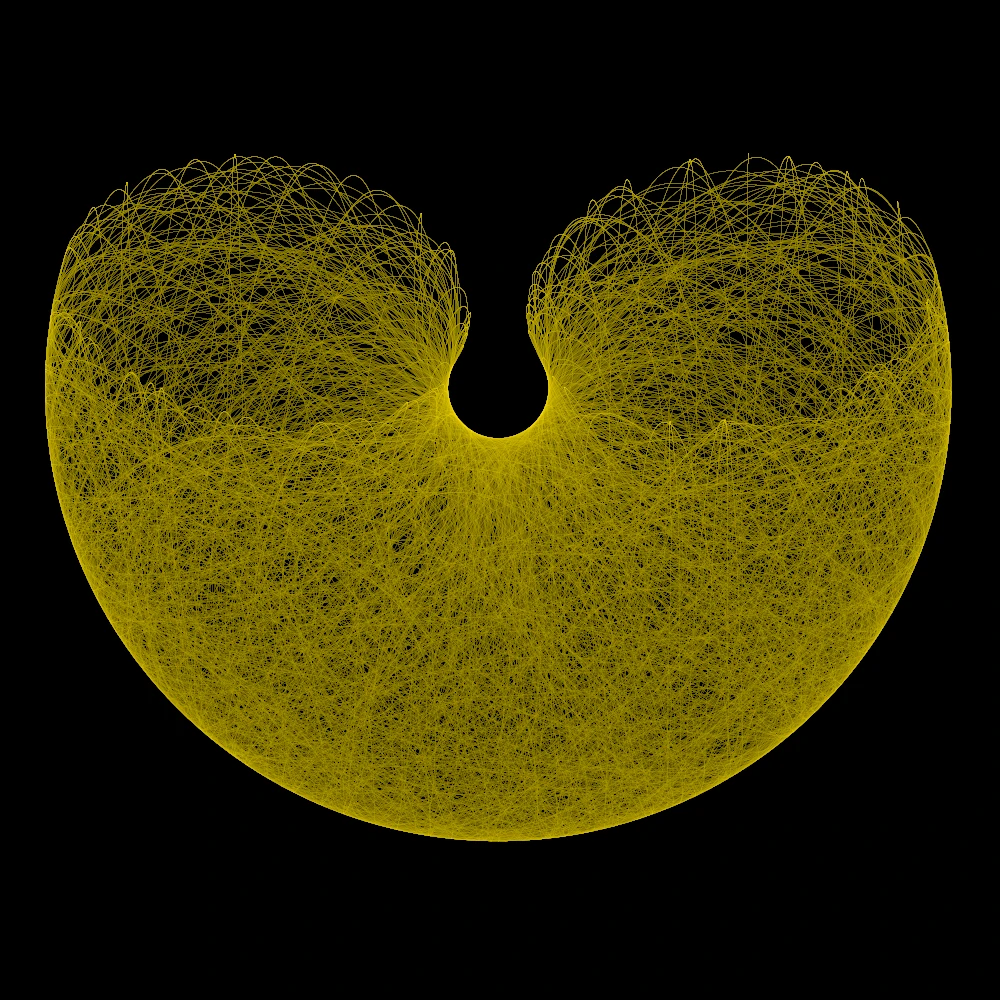
Möbius Flame
Diese Fraktale sind nahezu identisch zu den Fractal Flames, nur dass anstatt von
affinen Transformationen Möbius Transformationen auf der komplexen Ebene genutzt werden.

Wie findet man „gute“ Parameter?
Offenbar hat dieser Typ von Fraktal sehr viele freie Parameter. Um hübsche
Resultate zu generieren, müssen sie angepasst werden. Tatsächlich gibt es mit
electric sheep (ich hoffe stark, dass es eine
Blade Runner
Referenz ist) ein Crowdsourcing-Projekt,
das mithilfe von evolutionären Algorithmen und dem Feedback von Menschen
besonders ansehnliche Fraktale erzeugt.
Für mein Programm habe ich eine simplere Methode genutzt. Damit man ein Fraktal
gut sehen kann, sollte seine fraktale Dimension größer als 1 sein. Abschätzbar
ist es relativ einfach über die Korrelations-Dimension.
Dazu misst man die paarweisen Abstände von Punkten und misst den Exponenten ihrer
kumulativen Verteilungsfunktion.
Kombiniert mit einigen Heuristiken, die zu langgestreckte Fraktale verhindert,
sind die Ergebnisse meist ansprechend
Weitere Fraktale
Es gibt natürlich viel mehr Typen von Fraktalen. Auch wenn @AFractalADay
sie bisher nicht zeichnen kann, habe ich einige Bilder angefertigt, die ich
hier auch gerne zeigen möchte.
Diffusionsbegrenztes Wachstum
Diffusionsbegrenztes Wachstum bildet das Wachstum von Kristallen in stark
verdünnten Lösungen ab. Man startet mit einem Seed und lässt dann einzelne
Teilchen diffundieren, bis sie auf dem Nachbarfeld eines Seeds landen, wo sie
dann bleiben und Teil des Seeds werden. Dieser Prozess bildet verästelte
Strukturen aus.

Random Walks
Einige Arten von Random Walks haben eine fraktale Dimension zwischen 1 und 2,
was sie zu ansehnlichen Fraktalen machen sollte. Der Smart Kinetic Self
Avoiding Walk, der in meinem rsnake die Strategie des
Autopiloten ist, hat eine fraktale Dimension von . 100000 Schritte
sehen so aus: