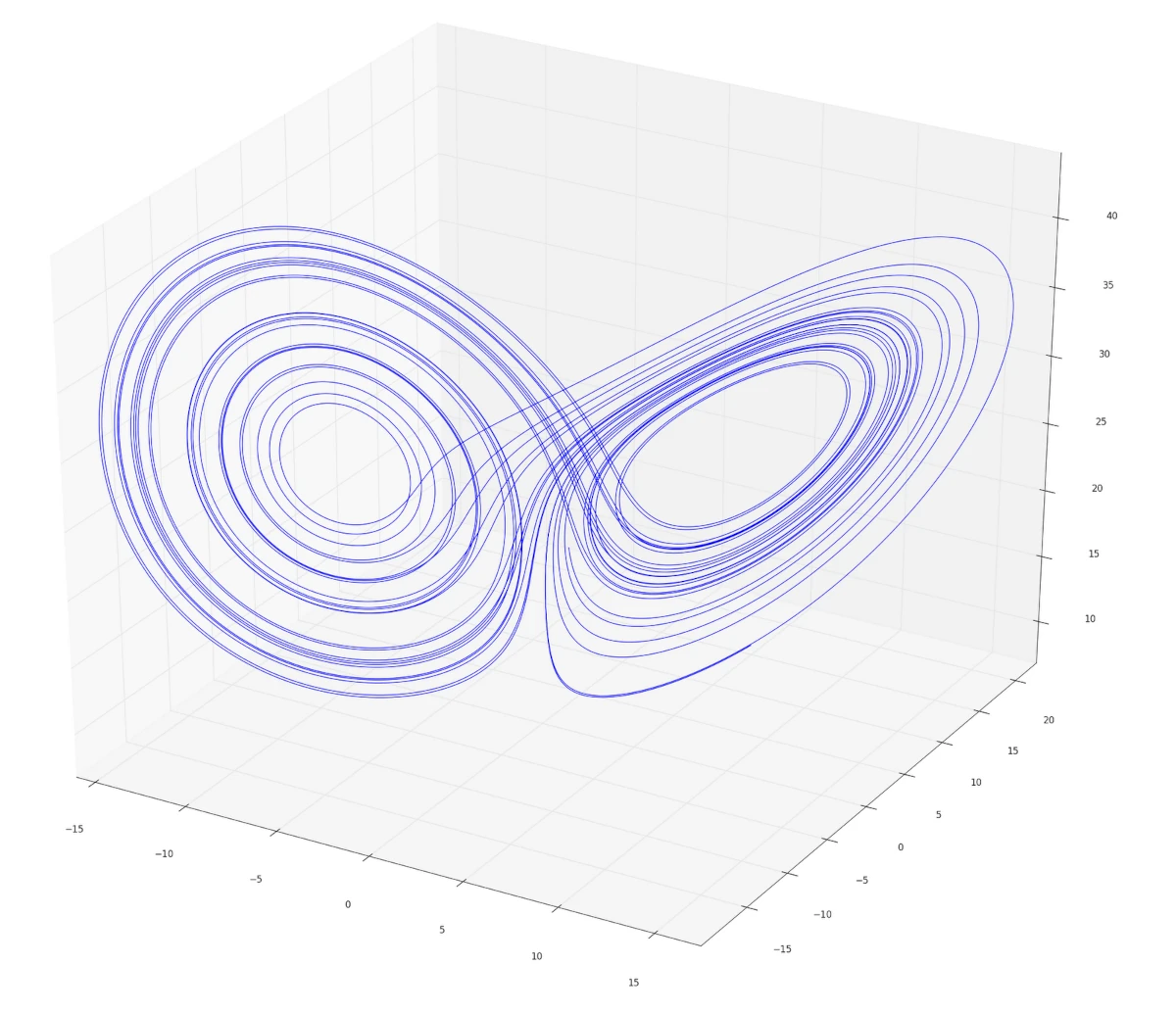
Seltsamer Attraktor
Zuvor habe ich bereits den Schmetterlingseffekt erwähnt. Um den Zusammenhang mit Chaos zu zeigen, betrachten wir folgendes Video von der Projektion in die y-z-Ebene von 13 Teilchen, die den Attraktor durchlaufen.
Alle Teilchen starten auf fast dem selben Punkt, aber nehmen sehr verschiedene Wege. Nach kurzer Zeit kann man den einzelnen Teilchen nicht mehr ansehen, dass sie fast die gleichen Anfangsbedingungen hatten.
Lorenz war Meteorologe und sein Differentialgleichungssystem \begin{align} \dot{X} &= a(Y - X) \ \dot{Y} &= X(b - Z) - Y \ \dot{Z} &= XY - cZ, \ \end{align} das dieses chaotische Verhalten zeigt, sollte die Atmosphäre modellieren.
Jetzt kann man verstehen, was es mit dem Schmetterling aus Jurassic Park auf sich hat.
Er bewegt in Peking die Flügel, und im Central Park gibt’s Regen statt Sonne.
— Dr. Ian Malcolm (1993)
Sein Flügelschlag ändert den Zustand eines chaotischen Systems, dem Wetter, ein wenig und nach einiger Zeit hat das System einen grundlegend anderen Weg eingeschlagen, als ohne diesen Flügelschlag.
Dennoch sieht das Video irgendwie geordnet aus. Fast schon vorhersagbar. Seltsam.