möchte­gern­geek

Vor kurzem habe ich angefangen „Think Complexity“ zu lesen — ein leicht verständliches, interessantes Buch, in dem unter anderem Zelluläre Automaten angesprochen werden. Und zwar die von Stephen Wolfram — ja der Stephen Wolfram, der Mathematica und Wolfram|Alpha entwickelt hat (vermutlich jedoch nicht allein). Zelluläre Automaten eignen sich natürlich sehr gut, pixelige Bilder zu erstellen, wie der Conways-Game-of-Life-Post beweist. Daher, lasse ich erstmal ein Bild sprechen.

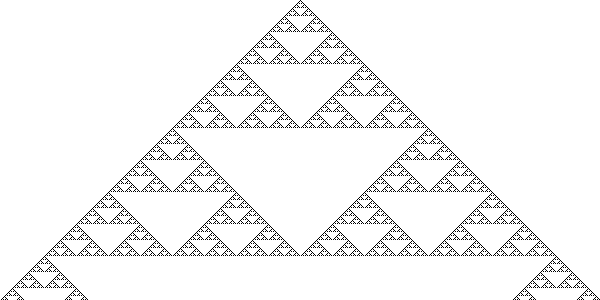
Die Idee ist, dass man mit einem eindimensionalen Zustand startet, und einen neuen Zustand daraus mit lokalen Regeln, die je einen rechten und linken Nachbarn berücksichtigen, erzeugt. Stellt man diese Zustände untereinander da, entstehen Strukturen, wie die, die an ein Sierpinski-Dreieck erinnert. Die Erklärung, wie genau diese Regeln lauten, und wie sie definiert sind, überlasse ich passenderweise Wolfram|Alpha.

Und damit ich auch etwas sage, das tiefsinnig erscheint: Die Dreieckige Form entspricht übrigens dem Vorwärtslichtkegel des Startwertes in der ersten Zeile. Die \(y\)-Achse entspricht hier schließlich einer Zeit und die „Lichtgeschwindigkeit“, mit der Beeinflussungen propagieren können, ist 1 Pixel pro Iteration.

Den Quellcode gibt es natürlich bei GitHub. Wenn auch nur in einem „kleine Fingerübungen in C“-Repo.

Für Liebhaber, hier noch eins im original 1982 Retro-Look.

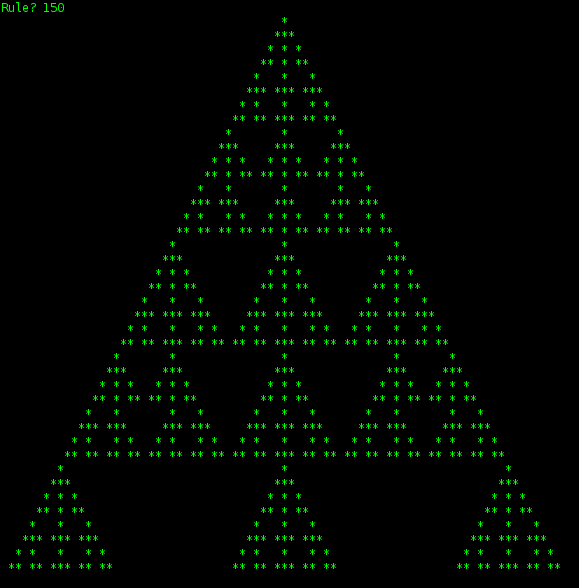
Passend zur Jahreszeit, wie ich finde.

Da nicht jeder das nötige Kleingeld für ein Oszilloskop und Funktionsgenerator hat, aber jeder gerne eine Lissajous-Figur laufen haben möchte, liefere ich hier den entsprechenden Gnuplot Code.

reset
set term gif animate optimize
set output "lissajous.gif"
n=6250

set xr [-1:1]
set yr [-1:1]

set parametric
unset border
unset xtics
unset ytics

fx(t) = sin(t)
fy(t) = sin(2.999*t)

i=0
load "animateLissajou.gp"
set output

Die Datei „animateLissajou.gp“ sieht dann so aus:

set trange [i:i+2*pi]
plot fx(t),fy(t) lc rgb 'black' notitle

i=i+2*pi*10
if (i < n) reread

Stark angelehnt an diesen Blogeintrag. Das Ergenis sieht dann so aus.

Wer kennt das nicht: Man hat sich ein Python Skript geschrieben, um seine Daten per Bootstrap Resampling auszuwerten und stellt fest, dass das Konstrukt zur Bildung des „Samples mit Ersetzungen“

    import random
    x = [1,2,3]

    bootstrapSample = [random.choice(x) for _ in x]

einfach nicht schnell genug ist.
Aber glücklicherweise gibt es numpy!

    import numpy
    x = [1,2,3]

    bootstrapSample = list(numpy.random.choice(x, len(x)))

Das ist — zumindest in meinem Anwendungsfall — spürbar schneller. Ich werde in Zukunft also immer optimale Fehlerbalken erzeugen.