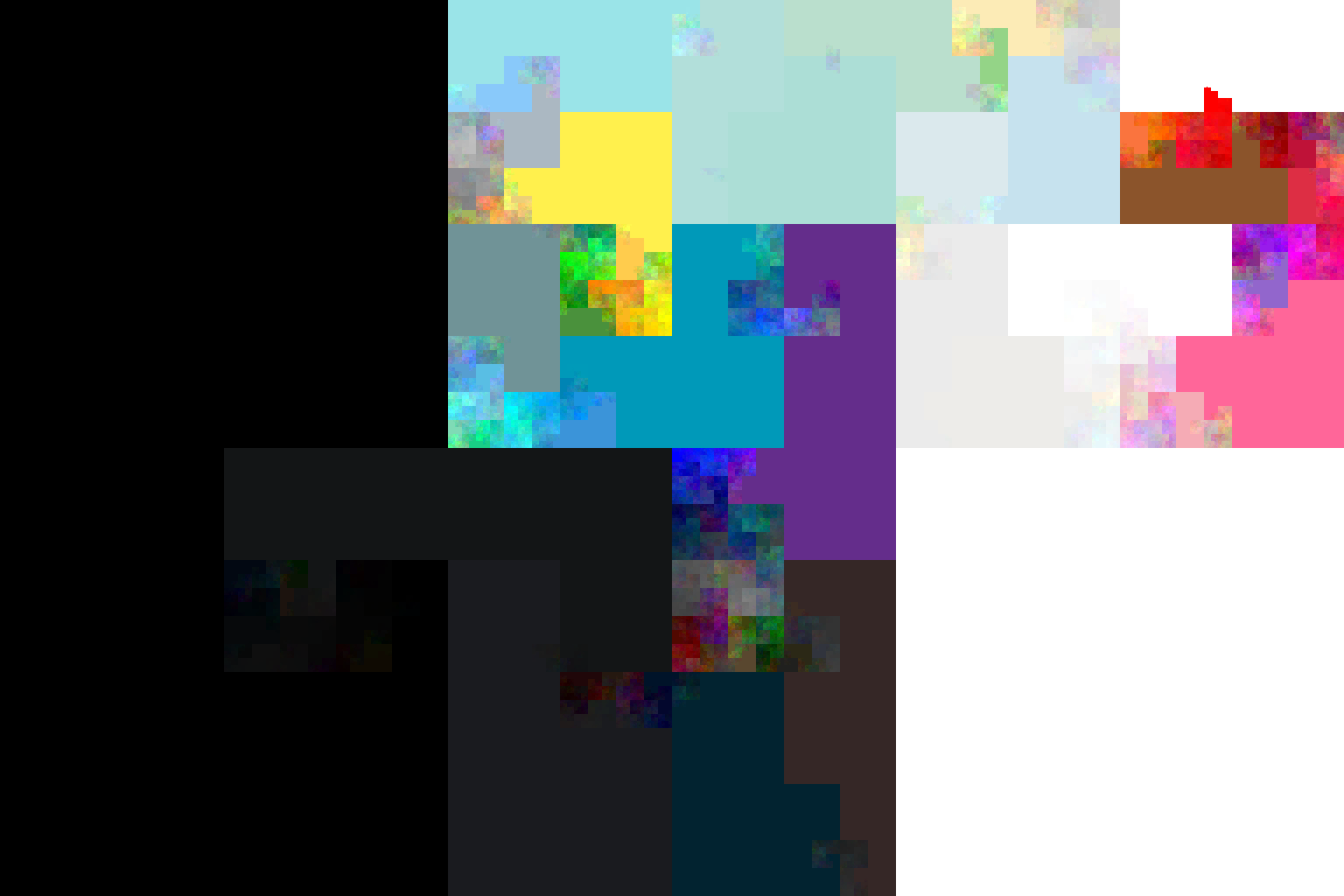I collected tweets of Twitter users for an academic project.
But Twitter does not only give you the tweets, but also many more data like
the profile background color of users. It would be a shame to let these data
go to waste, so I decided to process them into digital art. I wanted to show
all the colors in one picture and group similar colors close to each other.
This turned out to be much less trivial than I expected, since the space
in which the colors live is the three dimensional RGB cube, but my image is
only two dimensional. There is no “correct” way to project the colors down.
Here, I decided to put a 2D Hilbert curve
through the image and paint the colors in the order they are encountered by
a 3D Hilbert curve in the RGB cube. Ignoring the two default colors
#F5F8FA and #C0DEED, this produces this image:
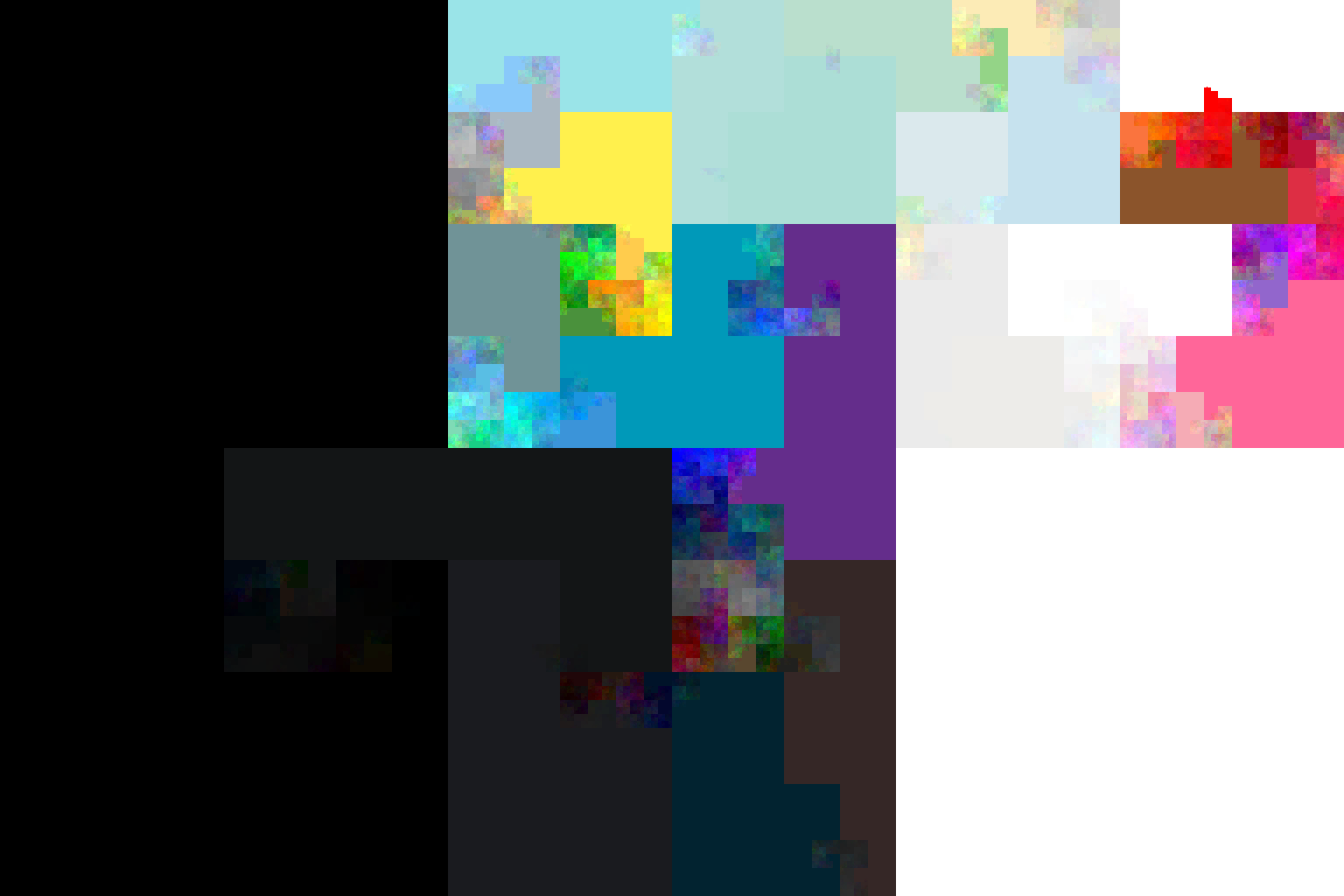
And thanks to the Python packages hilbertcurve and pypng the code needed
to generate this image is quite harmless:
from math import ceil, sqrt, log2
from hilbertcurve.hilbertcurve import HilbertCurve
import png
"""
turn an RGB string like `#C0DEED` into a tuple of integers,
i.e., coordinates of the RGB cube
"""
def str2rgb(s):
s = s.strip("#")
return (int(s[0:2], 16), int(s[2:4], 16), int(s[4:6], 16))
"""
`color_histogram` is a dict mapping an rgb string like `#F5F8FA`
to the number of usages of this color
"""
def plot_background_colors(color_histogram, filename="colors.png"):
defaults = {"F5F8FA", "C0DEED"}
data = {str2rgb(rgb): d for rgb, d in color_histogram if rgb not in defaults}
# calculate the size of the resulting image
# for a 2D Hilbert curve, it mus be square with a width, which is a power of 2
num_pixels = sum(data.values())
min_width = ceil(sqrt(num_pixels))
exponent = ceil(log2(min_width))
width = 2**exponent
# output buffer for a `width x width` png, with 4 color values per pixel
buf = [[0 for _ in range(4 * width)] for _ in range(width)]
hc2 = HilbertCurve(exponent, 2)
# there are 256 = 2^8 values in each direction of the RGB cube
hc3 = HilbertCurve(8, 3)
sorted_rgbs = sorted(data.keys(), key=lambda x: hc3.distance_from_point(x))
idx = 0
for rgb in sorted_rgbs:
for _ in range(data[rgb]):
# get the coordinate of the next pixel
x, y = hc2.point_from_distance(idx)
# assign the RGBA values to the pixel
buf[x][4 * y] = rgb[0]
buf[x][4 * y + 1] = rgb[1]
buf[x][4 * y + 2] = rgb[2]
buf[x][4 * y + 3] = 255
idx += 1
png.from_array(buf, 'RGBA').save(filename)
The input histogram was in my case just a simple SQL query away:
SELECT profile_background_color, COUNT(profile_background_color) FROM users
GROUP BY profile_background_color;