möchte­gern­geek

Seit meinem ersten Eintrag über meinen Fraktal-tweetenden Bot @AFractalADay, habe ich selbigen noch um ein paar Fraktale erweitert, die ich hier kurz festhalten möchte. Der ganze Code ist auf Github.

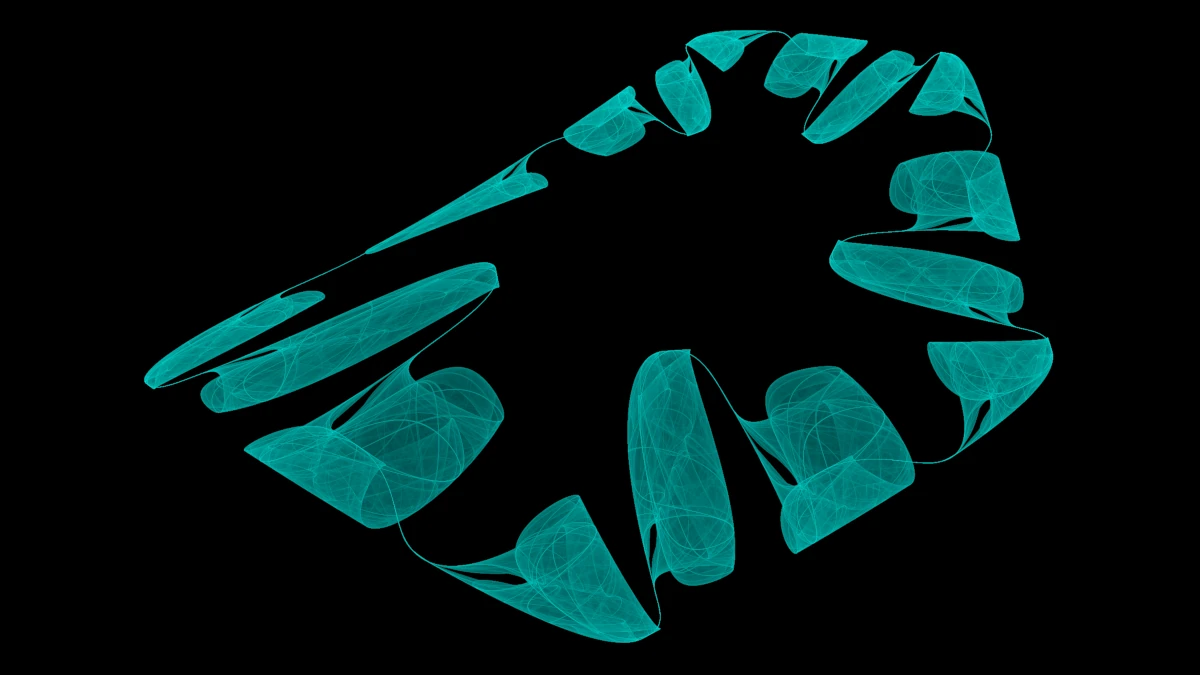
Chaotic Maps

Eine Quadratic Map ist eine Rekursionsgleichung mit einem quadratischen Term, also beispielsweise

Das berühmteste Mitglied dieser Familie ist die Logistic-Map mit \(a_0=1, a_1=r, a_2=0\), die chaotisches Verhalten für \(3.56995 < r < 4\) zeigt. Aber leider ist sie nur eindimensional und ihr Attraktor deshalb nicht besonders hübsch.

Um visuell ansprechende Fraktale daraus zu erzeugen, brauchen wir also ein System aus zwei Rekursionsgleichungen, die wir als \(x\)- und \(y\)-Koordinaten betrachten können:

Jetzt haben wir 12 freie Parameter, die einen riesigen Parameterraum aufspannen, in dem etwa 1.6% aller Möglichkeiten chaotisches Verhalten mit einem seltsamen Attraktor zeigen.

Chaotische Differentialgleichungssysteme

Ein echter Klassiker ist das Differentialgleichungssystem, das die Chaostheorie begründet hat und nach dem der Schmetterlingseffekt benannt ist [1, 2]. Für bestimmte Paramtersätze verlaufen die Bahnkurven entlang eines seltsamen Attraktors, dessen fraktale Dimension \(\approx 2.06\) ist. Da der vollständige Attraktor somit in einer zweidimensionalen Projektion etwas langweilig aussieht, habe ich hier nur eine Trajektorie über kurze Zeit dargestellt.

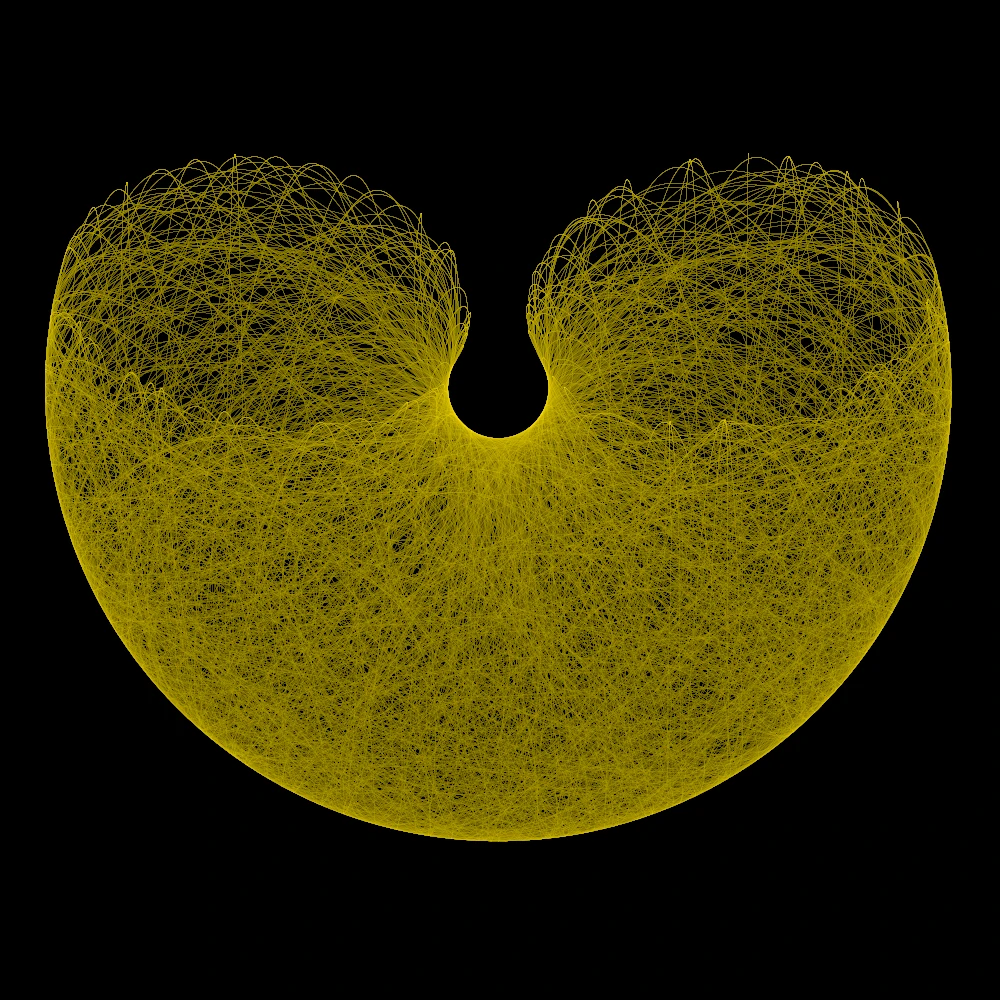
Und es gibt eine ganze Menge weitere Differntialgleichungssysteme (und chaotic maps), die chaotische Attraktoren aufweisen. Deshalb zeige ich hier noch einen Rössler-Attraktor, der eine vereinfachte Version des Lorenz-Systems ist:

Und hier haben wir das Glück, dass auch seine Projektion sehr ansehnlich ist.

Ich persönlich frage mich, nun wie der Attraktor für das Doppelpendel aussieht. Es ist anscheinend kein Fraktal, aber es sieht dennoch ganz interessant aus:

Ising model

Das Ising Modell für Ferromagnetismus wird auch als Drosophila der statistischen Physik bezeichnet: Es ist ein einfaches Modell, dass einen Phasenübergang aufweist — Eisen verliert seine magnetischen Eigenschaften oberhalb der Curie-Temperatur.

Es besteht aus magnetischen Momenten, Spins, die gerne in die gleiche Richtung zeigen wie ihre Nachbarn, aber durch hohe Temperatur gestört werden. Oder etwas formaler: Die innere Energie \(U\) wird durch den Hamiltonian \(\mathcal{H} = - \sum_{<ij>} s_i s_j\) bestimmt, wobei \(s_i = \pm 1\), je nachdem ob der Spin up oder down ist und die Summe über benachbarte Spins läuft. Das System wird immer einen Zustand anstreben, der die freie Energie \(F=U-TS\) minimiert. Das kann entweder passieren, indem \(U\) möglichst klein ist oder die Entropie \(S\) möglichst hoch. Bei großen Werten der Temperatur \(T\) bekommt der Entropie-Term ein höheres Gewicht, sodass Zustände mit hoher Entropie, also zufälligen Spinausrichtungen, bevorzugt sind, bei niedrigen Temperaturen werden Konfigurationen mit niedriger innerer Energie bevorzugt, also solche in denen alle Spins in die selbe Richtung zeigen. Die Temperatur, bei der sich beide Terme die Waage halten, nennt man kritische Temperatur. Hier bilden sich Regionen von Spins, die in die gleiche Richtung zeigen, auf allen Größenskalen. Die fraktale Dimension dieser Regionen ist 187/96, was solche kritische Konfigurationen interessant anzusehen macht. Ich empfehle auf das folgende Bild zu klicken und etwas hineinzuzoomen.

Für ein Projekt habe ich Tweets von >8‘000‘000 Twitter-Usern eingesammelt. Dabei fallen noch eine Reihe weiterer Daten an, wie die Profilhintergrundfarbe. Es wäre eine Schande diese Daten einfach verkommen zu lassen, also habe ich nach einer Möglichkeit gesucht diese Information ansprechend darzustellen, was sich als weniger trivial herausgestellt hat, als ich ursprünglich angenommen hatte: Im Idealfall sollten ähnliche Farben nahe beieinander liegen, allerdings ist der RGB Farbraum ein dreidimensionaler Kubus, ein Bild aber nur zweidimensional, sodass es keine „richtige“ Art und Weise gibt, ähnliche Farben nebeneinander anzuordnen.

Ich habe mich hier dafür entschieden eine 2D Hilbert-Kurve durch mein Bild zu legen und die Farben in der Reihenfolge zu zeichnen, in der eine 3D Hilbert-Kurve ihnen im RGB-Kubus begegnet. Wenn man dann noch die beiden Standardhintergrundfarben #F5F8FA und #C0DEED ignoriert, sieht das Ergebnis so aus.

Und dank der Python Pakete hilbertcurve und pypng ist der Code sogar ziemlich harmlos:

from math import ceil, sqrt, log2

from hilbertcurve.hilbertcurve import HilbertCurve
import png


"""
    turn an RGB string like `#C0DEED` into a tuple of integers,
    i.e., coordinates of the RGB cube
"""
def str2rgb(s):
    s = s.strip("#")
    return (int(s[0:2], 16), int(s[2:4], 16), int(s[4:6], 16))


"""
    `color_histogram` is a dict mapping an rgb string like `#F5F8FA`
    to the number of usages of this color
"""
def plot_background_colors(color_histogram, filename="colors.png"):
    defaults = {"F5F8FA", "C0DEED"}

    data = {str2rgb(rgb): d for rgb, d in color_histogram if rgb not in defaults}

    # calculate the size of the resulting image
    # for a 2D Hilbert curve, it mus be square with a width, which is a power of 2
    num_pixels = sum(data.values())
    min_width = ceil(sqrt(num_pixels))
    exponent = ceil(log2(min_width))
    width = 2**exponent

    # output buffer for a width x width png, with 4 color values per pixel
    buf = [[0 for _ in range(4 * width)] for _ in range(width)]

    hc2 = HilbertCurve(exponent, 2)
    # there are 256 = 2^8 values in each direction of the RGB cube
    hc3 = HilbertCurve(8, 3)

    sorted_rgbs = sorted(data.keys(), key=lambda x: hc3.distance_from_point(x))

    idx = 0
    for rgb in sorted_rgbs:
        for _ in range(data[rgb]):
            # get the coordinate of the next pixel
            x, y = hc2.point_from_distance(idx)
            # assign the RGBA values to the pixel
            buf[x][4 * y] = rgb[0]
            buf[x][4 * y + 1] = rgb[1]
            buf[x][4 * y + 2] = rgb[2]
            buf[x][4 * y + 3] = 255

            idx += 1

    png.from_array(buf, 'RGBA').save(filename)

Das Histogram, das als Input benötigt wird war in meinem Fall nur eine SQL Query entfernt:

SELECT profile_background_color, COUNT(profile_background_color) FROM users
    GROUP BY profile_background_color;

Für jeden Zweck das passende Werkzeug: In meinem Alltag bedeutet das, dass ich Simulationen in Rust schreibe und in Python visualisiere. Dank inline-python geht das sogar sehr reibungslos.

use inline_python::python;

fn main() {
    let x: Vec<f32> = (0..628).map(|i| i as f32 / 100.).collect();
    let y: Vec<f32> = x.iter().map(|x| x.sin()).collect();

    python! {
        import numpy as np
        from matplotlib import pyplot as plt

        plt.plot('x, 'y)
        plt.show()
    }
}

Dieses Minimalbeispiel ist natürlich nicht nützlich, aber ich habe es bereits produktiv genutzt, um Dynamik auf petgraph Graphen zu simulieren und ihren Zustand per graph-tool zu visualisieren.