Vicsek
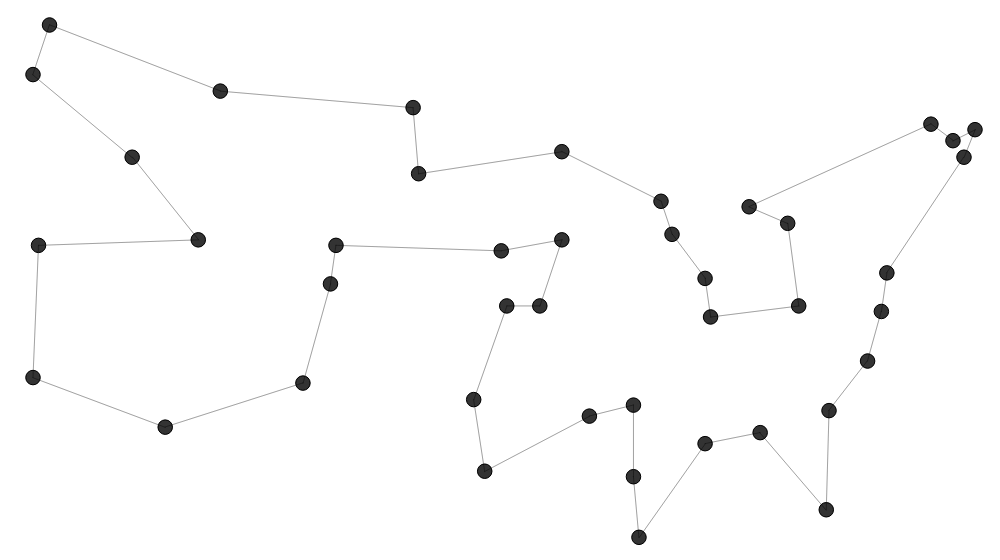
Das Vicsek-Modell wurde 1995 vorgeschlagen, um das Schwarmverhalten von Vögeln oder Fischen zu modellieren. Die Idee ist, dass jedes Individuum seine Bewegungsrichtung an der seiner Nachbarn anpasst. Wenn jedes Individuum genügend Nachbarn hat und die Störeinflüsse nicht zu groß sind, bilden sich Schwärme. Videos von solchen Schwärmen werden auf allen größeren Konferenzen der Statistischen Physik gezeigt — und jetzt auch hier.
Auf GitHub findet sich das Programm, das ich für obiges Video geschrieben habe. Es ist in Rust geschrieben und zeigt die Simulation per Piston auf dem Bildschirm.
Ich habe sehr großen Gefallen an Rust gefunden — gerade für ein Projekt wie dieses scheint es ideal geeignet. Es ist so schnell wie C, aber man muss sich keinerlei Gedanken um den Speicher machen und einige andere Fehlerklassen, die der Compiler direkt verhindert. Rayon macht Parallelisierung so einfach wie OpenMP — mit dem Vorteil, dass der Compiler einen Fehler ausgibt, falls es eine Variable gibt, aus der parallel gelesen und geschrieben wird.
Als Beispiel, warum ich Rust als sehr leserlich und elegant empfinde, möchte ich folgendes (unvollständige) Beispiel ansehen.
pub enum Proximity {
Neighbors(usize),
Radius(f64)
}
pub struct Vicsek {
proximity: Proximity,
}
impl Vicsek {
fn update(bird: &mut Bird) {
match self.proximity {
Proximity::Neighbors(n) => self.update_direction_neighbors(bird, n, noise),
Proximity::Radius(r) => self.update_direction_disk(bird, r, noise),
}
}
}
Die Methode update() passt die Richtung an, in die ihr Argument im nächsten
Zeitschritt fliegen soll. In meiner Simulation gibt es zwei Möglichkeiten:
entweder orientiert man sich an seinen n nächsten Nachbarn oder an allen
Vögeln innerhalb eines Radius von r. Der Datentyp Proximity kann eines von
beiden beinhalten — welches vorhanden ist, kann elegant per Pattern-Matching
ermittelt werden.
Brauche ich länger, um Rust zu schreiben als C oder C++? Vermutlich, aber ich verbringe weniger Zeit mit dem Debuggen. Netto also mehr Spaß.
Das sind 42 Hauptstädte der Vereinigten Staaten von Amerika und Washington, 
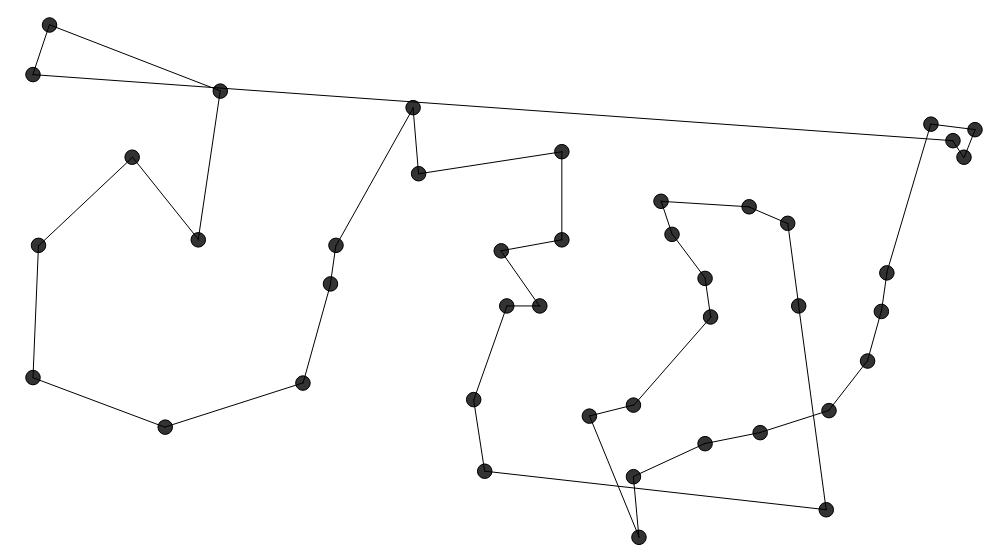Die Nearest Neighbor Heuristik (
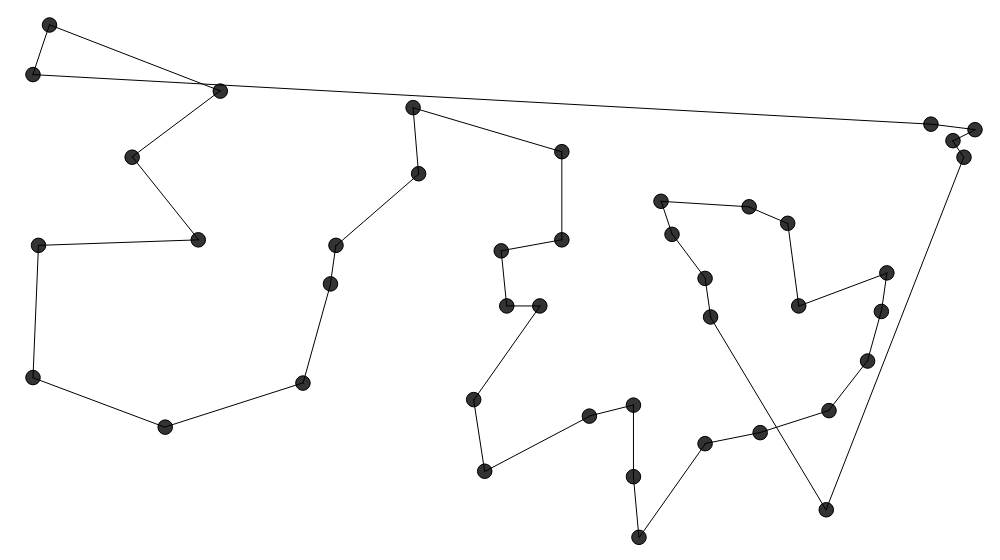Diese Heuristik (
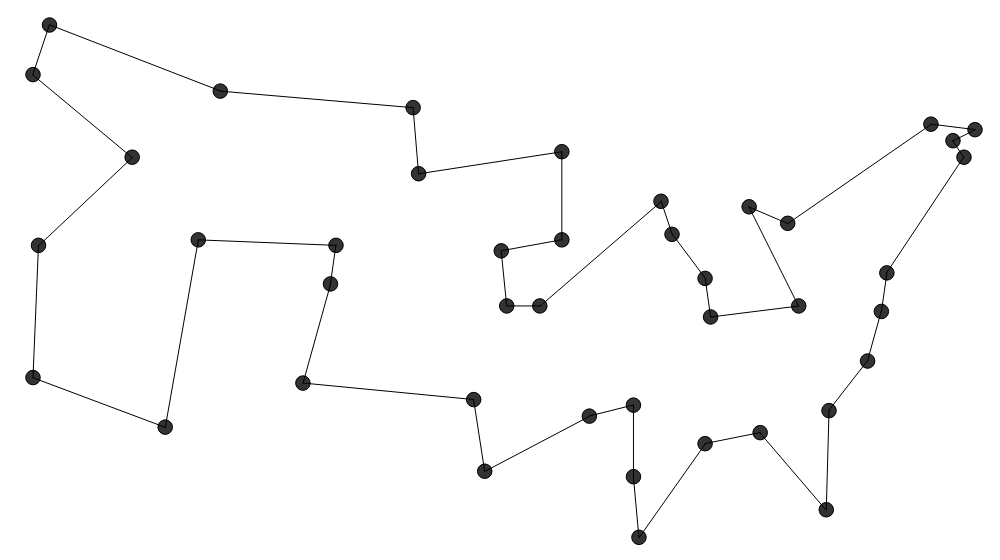Farthest Insertion (
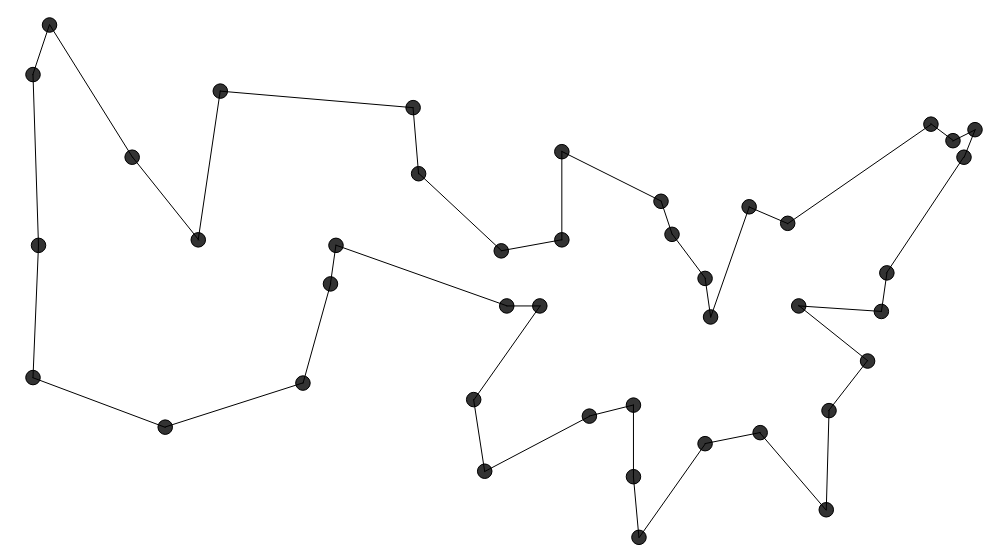Two-Opt beginnt mit einer beliebigen Tour, die bspw. durch eine der obigen
Heuristken erstellt wurde und verbessert sie, indem sie zwei Verbindungen nimmt
und die Endpunkte über Kreuz austauscht, wenn die Tour dadurch verbunden bleibt
und kürzer wird.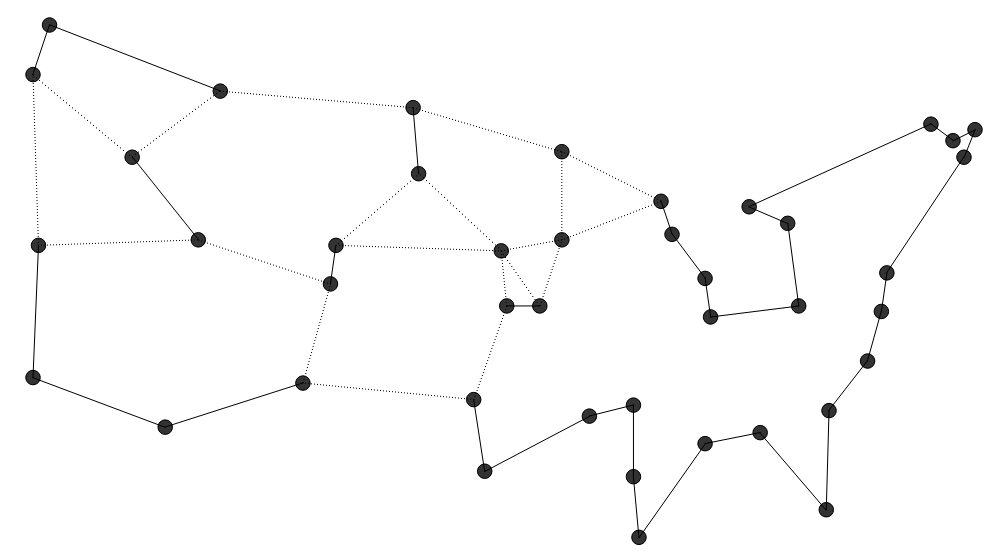
Lineare Programmierung (